目录

分割字符串的最大得分

给你一个由若干 0 和 1 组成的字符串 s ，请你计算并返回将该字符串分割成两个 非空 子字符串（即 左 子字符串和 右 子字符串）所能获得的最大得分。

「分割字符串的得分」为 左 子字符串中 0 的数量加上 右 子字符串中 1 的数量。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-score-after-splitting-a-string

示例

输入：s = “011101”
输出：5
解释： 将字符串 s 划分为两个非空子字符串的可行方案有：
左子字符串 = “0” 且 右子字符串 = “11101”，得分 = 1 + 4 = 5
左子字符串 = “01” 且 右子字符串 = “1101”，得分 = 1 + 3 = 4
左子字符串 = “011” 且 右子字符串 = “101”，得分 = 1 + 2 = 3
左子字符串 = “0111” 且 右子字符串 = “01”，得分 = 1 + 1 = 2
左子字符串 = “01110” 且 右子字符串 = “1”，得分 = 2 + 1 = 3

我的思路

利用Python的冒号分割和count()函数。
看漏要求左右字串都是非空子集而被罚时。 因为count()是O(n)的，故整体是O(n**2)的，但未超时

我的代码

1
2
3
4
5
6
7
8

class Solution:
    def maxScore(self, s: str) -> int:
        res = 0
        for i in range(1, len(s)):
            tmp = s[:i].count("0") + s[i:].count("1")
            if tmp > res:
                res = tmp
        return res

别人的思路

先统计字符串中1的个数，然后从左往右遍历，当为1时，1的个数减1，0的个数加1，每次求和留最大值。
时间复杂度降低为O(n)

别人的代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution:
    def maxScore(self, s: str) -> int:
        res, c0, c1 = 0, 0, 0
        for ch in s:
            if ch == '1':
                c1 += 1
        for i in range(len(s) - 1):
            if s[i] == '1':
                c1 -= 1
            else:
                c0 += 1
            res = max(res, c1 + c0)
        return res

可获得的最大点数

几张卡牌 排成一行，每张卡牌都有一个对应的点数。点数由整数数组 cardPoints 给出。

每次行动，你可以从行的开头或者末尾拿一张卡牌，最终你必须正好拿 k 张卡牌。

你的点数就是你拿到手中的所有卡牌的点数之和。

给你一个整数数组 cardPoints 和整数 k，请你返回可以获得的最大点数。

提示：

  • 1 <= cardPoints.length <= 10^5
  • 1 <= cardPoints[i] <= 10^4
  • 1 <= k <= cardPoints.length

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-points-you-can-obtain-from-cards

示例

输入：cardPoints = [1,2,3,4,5,6,1], k = 3
输出：12
解释：第一次行动，不管拿哪张牌，你的点数总是 1 。但是，先拿最右边的卡牌将会最大化你的可获得点数。最优策略是拿右边的三张牌，最终点数为 1 + 6 + 5 = 12 。

我的思路

用dfs递归，每次往左右两边选数的方向递归，直至选了k个数后退出递归。最后超时。

别人的思路

先求左边k个数的和 tmp。时间复杂度为O(k) 。 如果右边选了一个数，那么左边只能选k-1个数。因此此时的和为 tmp 减去左边第k个数再加上右边第一个数，记为新的 tmp。
同理，如果右边选了两个数，那么左边只能选k-2个数。因此此时的和为新的 tmp 减去左边第k-1个数再加上右边第二个数，继续以此更新 tmp。
循环k次。故总体时间复杂度为O(2k)。

别人的代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution:
    def maxScore(self, cardPoints: List[int], k: int) -> int:
        res, tmp = 0, 0
        for i in range(k):
            tmp += cardPoints[i]
        res = tmp # 左边k个数的和也要加入比较
        left, right = k - 1, len(cardPoints) - 1
        while left >= 0:
            tmp = tmp - cardPoints[left] + cardPoints[right]
            res = max(res, tmp)
            left -= 1
            right -= 1
        return res

对角线遍历ii

给你一个列表 nums ，里面每一个元素都是一个整数列表。请你依照下面各图的规则，按顺序返回 nums 中对角线上的整数。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/diagonal-traverse-ii/

示例

示例

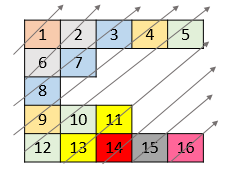
输入：nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]]
输出：[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]

别人的思路

首先可以看到每条对角线对应的位置的横纵坐标和是递增且唯一的，如第一条对角线的横纵坐标和为0，第二条对角线的横纵坐标和为1，第三条的为2…
而具体对每一条对角线，列数越小的越在前。
因此，可以将每个元素的信息做一个元组，元组结构为（行列和值，列值，数值）。将这些元组做成一个列表并用sort()进行排序，sort()默认按元组从左到右的构成进行排序。

别人的代码

1
2
3
4
5
6
7
8

class Solution:
    def findDiagonalOrder(self, nums: List[List[int]]) -> List[int]:
        tmp = []
        for i in range(len(nums)):
            for j in range(len(nums[i])):
                tmp.append((i + j, j, nums[i][j]))
        tmp.sort()
        return [x[2] for x in tmp]

带限制的子序列和

给你一个整数数组 nums 和一个整数 k ，请你返回 非空 子序列元素和的最大值，子序列需要满足：子序列中每两个 相邻 的整数 nums[i] 和 nums[j] ，它们在原数组中的下标 i 和 j 满足 i < j 且 j - i <= k 。

数组的子序列定义为：将数组中的若干个数字删除（可以删除 0 个数字），剩下的数字按照原本的顺序排布。

提示：

  • 1 <= k <= nums.length <= 10^5
  • -10^4 <= nums[i] <= 10^4

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/constrained-subset-sum

示例

输入：nums = [10,-2,-10,-5,20], k = 2
输出：23
解释：子序列为 [10, -2, -5, 20]

别人的思路

动态规划+单调栈。
dp[i]表示以第i个值为结尾的最大子序列和，则有转移状态方程：dp[i] = max(nums[i], max(dp[j]) + nums[i])，其中 max(0, i - k) <= j <= i - 1。 用单调栈维护最大dp[j]的索引，实现查询最大dp[j]时的时间复杂度为O(1)

别人的代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

class Solution:
    def constrainedSubsetSum(self, nums: List[int], k: int) -> int:
        n = len(nums)
        dp = [0] * n
        dp[0] = nums[0] # 因为子序列非空
        res = nums[0]
        # 单调栈记录dp[i]的索引值，越在左边，对应的dp[i]越大，即stack[0]表示当前栈中最大的dp[i]
        stack = [0] 
        for i in range(1, n):
            dp[i] = max(nums[i], dp[stack[0]] + nums[i])
            while stack and dp[stack[-1]] <= dp[i]:
                stack.pop() # 维护stack单调递减
            stack.append(i)
            # 这个等号：如k=2，索引3-索引1等于，但之间有3个值，故用等号限定为两个值
            while i - stack[0] >= k: 
                stack.pop(0) # 维护栈内最大dp的索引与当前索引距离不超过k
            res = max(res, dp[i])
        return res

总结

LeetCode的周赛和大头菜贩卖时间冲突就很蛋疼。
做前三题被罚时太多就没继续做了，只AC第一题，排名1300/3107。