目录
用栈操作构建数组
给你一个目标数组 target 和一个整数 n。每次迭代,需要从 list = {1,2,3…, n} 中依序读取一个数字。
请使用下述操作来构建目标数组 target :
Push:从 list 中读取一个新元素, 并将其推入数组中。
Pop:删除数组中的最后一个元素。
如果目标数组构建完成,就停止读取更多元素。
题目数据保证目标数组严格递增,并且只包含 1 到 n 之间的数字。
请返回构建目标数组所用的操作序列。
题目数据保证答案是唯一的。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/build-an-array-with-stack-operations
示例
输入:target = [1,3], n = 3
输出:[“Push”,“Push”,“Pop”,“Push”]
解释:
读取 1 并自动推入数组 -> [1]
读取 2 并自动推入数组,然后删除它 -> [1]
读取 3 并自动推入数组 -> [1,3]
我的思路
对 [1, n] 的范围进行遍历,用一个cnt记录已填进target的数的数目。如果当前遍历到的数不在target内,则用push加pop操作;如果当前遍历到的数在target内,则push该数,cnt加1。
当cnt超过target数组长度时说明已完成target的构建,退出遍历。(这里没考虑到被罚时了)
仅遍历一次,时间复杂度O(n)
我的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution:
def buildArray(self, target: List[int], n: int) -> List[str]:
res = []
cnt = 0
for i in range(1, n + 1):
try:
if target[cnt] != i:
res += ["Push","Pop"]
else:
res += ["Push"]
cnt += 1
except:
break
return res
|
形成两个异或相等数组的三元组数目
给你一个整数数组 arr 。
现需要从数组中取三个下标 i、j 和 k ,其中 (0 <= i < j <= k < arr.length) 。
a 和 b 定义如下:
a = arr[i] ^ arr[i + 1] ^ … ^ arr[j - 1]
b = arr[j] ^ arr[j + 1] ^ … ^ arr[k]
注意:^ 表示 按位异或 操作。
请返回能够令 a == b 成立的三元组 (i, j , k) 的数目。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/count-triplets-that-can-form-two-arrays-of-equal-xor
示例
输入:arr = [2,3,1,6,7]
输出:4
解释:满足题意的三元组分别是 (0,1,2), (0,2,2), (2,3,4) 以及 (2,4,4)
我的思路
四重循环求a和b,时间复杂度O(n^4),超时
我的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution:
def countTriplets(self, arr: List[int]) -> int:
res = 0
for k in range(1, len(arr)):
for j in range(1, k + 1):
for i in range(j):
a, b = arr[i], arr[j]
for t in range(i + 1, j):
a ^= arr[t]
for t in range(j + 1, k + 1):
b ^= arr[t]
if a == b:
res += 1
return res
|
别人的思路
a^b = a[i]^a[i+1]^…^a[k];
如果a=b,则异或运算a^b = 0(异或,相同为0,不同为非0);
故对不同i,对不同k,如果满足a^b=0,则中间有k-i种j可以满足条件。
遍历i和k,时间复杂度O(n^2)
别人的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution:
def countTriplets(self, arr) -> int:
if len(arr) < 2:
return 0
n = len(arr)
res = 0
for i in range(n):
tmp = arr[i]
for k in range(i + 1, n):
tmp ^= arr[k]
if tmp == 0:
res += k - i
return res
|
收集树上所有苹果的最少时间
给你一棵有 n 个节点的无向树,节点编号为 0 到 n-1 ,它们中有一些节点有苹果。通过树上的一条边,需要花费 1 秒钟。你从 节点 0 出发,请你返回最少需要多少秒,可以收集到所有苹果,并回到节点 0 。
无向树的边由 edges 给出,其中 edges[i] = [fromi, toi] ,表示有一条边连接 from 和 toi 。除此以外,还有一个布尔数组 hasApple ,其中 hasApple[i] = true 代表节点 i 有一个苹果,否则,节点 i 没有苹果。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/minimum-time-to-collect-all-apples-in-a-tree
示例
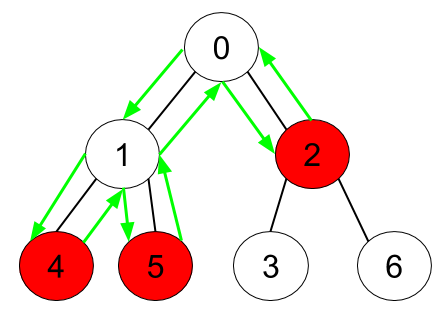
输入:n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
输出:8
解释:上图展示了给定的树,其中红色节点表示有苹果。一个能收集到所有苹果的最优方案由绿色箭头表示。
我的思路
首先遍历 edges 用字典 tree 存储各个节点对应层数,O(n);
然后遍历 tree 得到最大层数,O(n);其实可以在遍历edges时就可以做到;
声明存储索引即对应层数的level,如level[2]表示存储第2层节点的列表;以及存储每层需要经过的节点个数levelCnt,如levelCnt[2]表示存储第2层需要经过的节点个数;
再次遍历 tree 得到每层的节点,O(n);
从底层往上遍历level,遍历每层level的节点nodes,并遍历 edges 找到 node 的父节点,标记为需要经过的节点,O(m * n^2), m为level层的节点数;
遍历 levelCnt,每层需要的时间 = 该层需要经过的节点数 * 2。
总的时间复杂度 O(m * n^2), 超时。
我的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution:
def minTime(self, n: int, edges, hasApple) -> int:
if len(set(hasApple)) == 1 and hasApple[0] == False:
return 0
tree = {0: 0}
for edge in edges:
tree[edge[1]] = tree[edge[0]] + 1
maxLevel = 0
for k, v in tree.items():
if v > maxLevel:
maxLevel = v
level = [[] for i in range(maxLevel + 1)]
levelCnt = [0 for i in range(maxLevel + 1)]
for k, v in tree.items():
level[v].append(k)
for i in range(maxLevel, -1, -1):
for node in level[i]:
if hasApple[node] == True:
for edge in edges:
if edge[1] == node:
hasApple[edge[0]] = True
break
levelCnt[i] += 1
res = 0
for i in range(1, maxLevel + 1):
res += 2 * levelCnt[i]
return res
|
别人的思路
钻了用例的空子。用例的路径都是从根往叶遍历。
从后往前遍历路径,即从叶往根遍历树,孩子节点是苹果,则必会经过其父节点,故父节点也等同于有苹果,设为True。
再从根往叶遍历重新设置过的路径,除根节点外,每个为True的节点都要经过2次。
别人的代码
1
2
3
4
5
6
7
8
9
10
|
class Solution:
def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:
res = 0
for i in range(len(edges) - 1, -1, -1):
if hasApple[edges[i][1]] == True:
hasApple[edges[i][0]] = True
for i in range(len(edges)):
if hasApple[edges[i][1]] == True:
res += 2
return res
|
切披萨的方案数
给你一个 rows x cols 大小的矩形披萨和一个整数 k ,矩形包含两种字符: ‘A’ (表示苹果)和 ‘.’ (表示空白格子)。你需要切披萨 k-1 次,得到 k 块披萨并送给别人。
切披萨的每一刀,先要选择是向垂直还是水平方向切,再在矩形的边界上选一个切的位置,将披萨一分为二。如果垂直地切披萨,那么需要把左边的部分送给一个人,如果水平地切,那么需要把上面的部分送给一个人。在切完最后一刀后,需要把剩下来的一块送给最后一个人。
请你返回确保每一块披萨包含 至少 一个苹果的切披萨方案数。由于答案可能是个很大的数字,请你返回它对 10^9 + 7 取余的结果。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/number-of-ways-of-cutting-a-pizza
示例
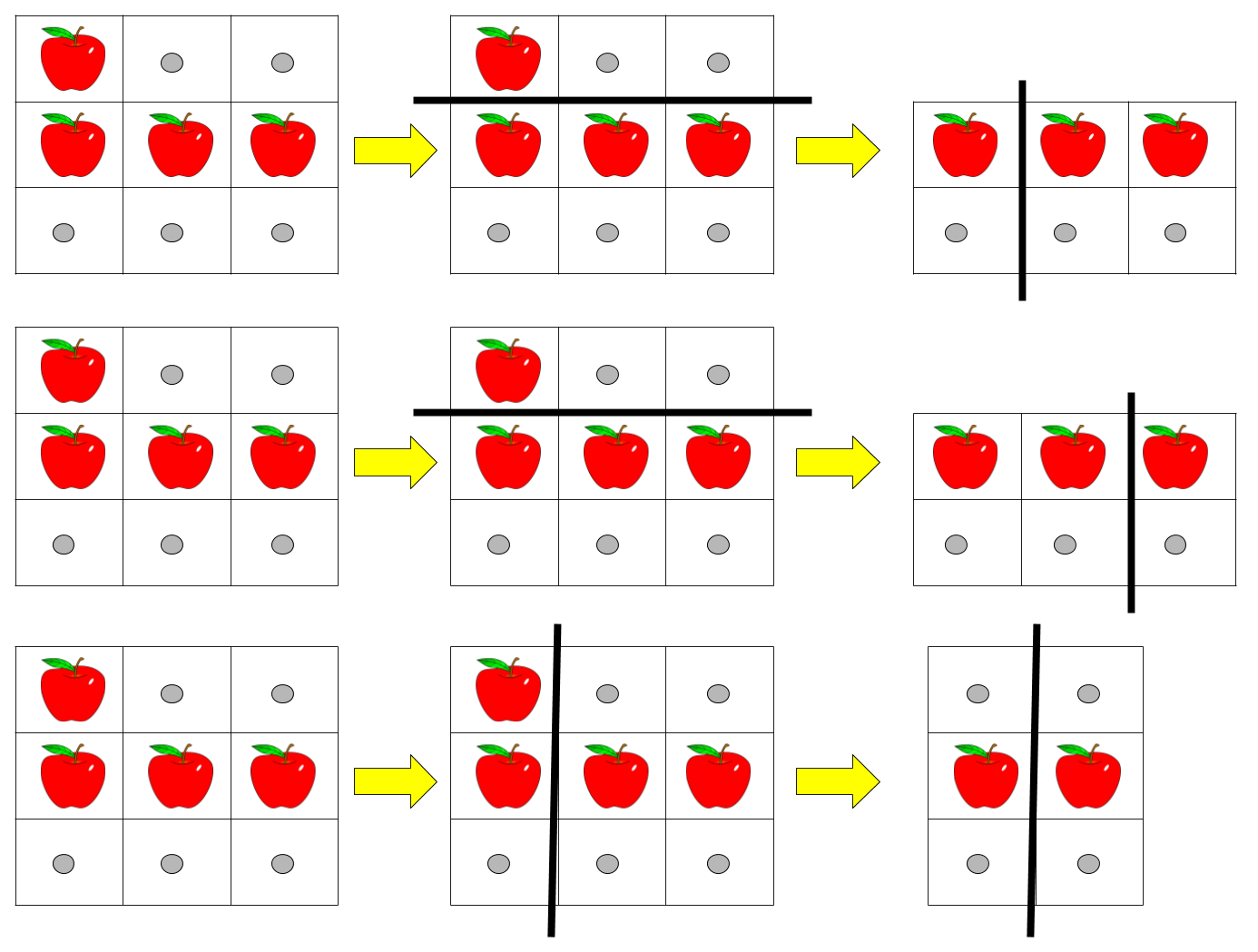
输入:pizza = [“A..”,“AAA”,”…"], k = 3
输出:3
解释:上图展示了三种切披萨的方案。注意每一块披萨都至少包含一个苹果。
别人的思路
先用二维前缀和求得以(0,0)为左上角,(i,j)为右下角的区域内的苹果数num[i][j];
然后DFS+DP穷举水平切和垂直切后有苹果的情况,dp[i][j][x]表示剩余披萨左上角坐标为(i,j)时,已切出x块。
状态转移方程为dp[i][j][x] += dp[row][col][x - 1], 该式于原来的以(row,col)为左上角的披萨被切为以(i,j)为左上角的一部分和剩余部分都包含苹果时成立。
别人的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
class Solution:
def ways(self, pizza, k: int) -> int:
row = len(pizza)
col = len(pizza[0])
mod = 10 ** 9 + 7
## 动态规划求num,num是二维前缀和
num = [[0 for i in range(col)] for i in range(row)] # num[i][j] 表示以[0][0]为左上角,[i][j]为右下角的区域包含的苹果数
if pizza[0][0] == 'A':
num[0][0] = 1
for i in range(1, row):
num[i][0] = num[i - 1][0] + (pizza[i][0] == 'A')
for i in range(1, col):
num[0][i] = num[0][i - 1] + (pizza[0][i] == 'A')
for i in range(1, row):
for j in range(1, col):
num[i][j] = num[i - 1][j] + num[i][j - 1] - num[i - 1][j - 1] + (pizza[i][j] == 'A')
def hasA(num, sr, sc, er, ec):
"""
判断该区域是否有苹果
(sr, sc): 该区域的左上角坐标
(er, ec): 该区域的右下角坐标
"""
num1 = 0 # num2和num3的交叉区域的苹果数
num2 = 0 # 待判断区域上面的区域内苹果数
num3 = 0 # 待判断区域左面的区域内苹果数
if sr != 0 and sc != 0:
num1 = num[sr - 1][sc - 1]
if sr != 0:
num2 = num[sr - 1][ec]
if sc != 0:
num3 = num[er][sc - 1]
return num[er][ec] - num2 - num3 + num1 > 0
dp = [[[0 for i in range(k + 1)] for i in range(col)] for i in range(row)] # dp[i][j][k] 代表剩余披萨的左上角坐标为[i][j]时,已切分的披萨数
dp[0][0][1] = 1
for x in range(2, k + 1):
for i in range(row):
for j in range(col):
if dp[i][j][x - 1] == 0:
continue
# 水平切
for z in range(i + 1, row):
if hasA(num, i, j, z - 1, col - 1) and hasA(num, z, j, row - 1, col - 1):
dp[z][j][x] += dp[i][j][x - 1]
dp[z][j][x] %= mod
# 垂直切
for z in range(j + 1, col):
if hasA(num, i, j, row - 1, z - 1) and hasA(num, i, z, row - 1, col - 1):
dp[i][z][x] += dp[i][j][x - 1]
dp[i][z][x] %= mod
res = 0
for i in range(row):
for j in range(col):
res += dp[i][j][k]
res %= mod
return res
|
总结
太弱了,没法总结。

