目录
检查单词是否为句中其他单词的前缀
给一个按空格分隔单词的句子sentence,给一个检索词searchWord
判断sentence里是否有以searchWord为前缀的单词,如果有则返回满足条件的第一个单词的位置,如果没有满足条件的单词则返回-1。
示例
输入:
sentence = “this problem is an easy problem”,
searchWord = “pro”
输出:2
解释:“pro” 是 “problem” 的前缀,而 “problem” 是句子中第 2 个也是第 6 个单词,但是应该返回最小下标 2 。
思路
遍历句子单词,如果单词长度不如检索词长则直接跳过;
从第一个字母开始对比单词和检索词,如果能匹配则直接返回当前单词的索引,否则继续遍历搜索;
搜索不到则返回-1。时间复杂度O(n*L),L为检索词长度
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution:
def isPrefixOfWord(self, sentence: str, searchWord: str) -> int:
words = sentence.split()
isFind = False
for i in range(len(words)):
if len(searchWord) > len(words[i]):
continue
for j in range(len(searchWord)):
if j == len(searchWord) - 1 and searchWord[j] == words[i][j]:
return i + 1
elif searchWord[j] == words[i][j]:
continue
else:
break
return -1
|
思路2
用枚举返回索引,用startswith()判断前缀
代码2
1
2
3
4
5
6
|
class Solution:
def isPrefixOfWord(self, sentence: str, searchWord: str) -> int:
for i, word in enumerate(sentence.split(), start=1):
if word.startswith(searchWord):
return i
return -1
|
定长子串中元音的最大数目
给一个字符串s和整数k,求s里长度不超过k的子串中包含的最大元音个数
示例
输入:s = “leetcode”, k = 3
输出:2
解释:“lee”、“eet” 和 “ode” 都包含 2 个元音字母。
思路
双指针start和end,遍历过程中保证end和start的差距不超过k。
每次end先前进到与start距离为k的位置,然后start再跟上来,不过先跟到范围内距离end最远的元音处,然后end再往前找,这时start抛弃当前元音,往前走一步。重复此过程。
因为start可能会跟着end都走到字符串末尾,时间复杂度O(5*n^2),其中5是查询当前指针所指字母是否元音的时间复杂度。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution:
def maxVowels(self, s: str, k: int) -> int:
tmp = ["a","e","i","o","u"]
start, end = 0, 0
res = 0 if s[start] not in tmp else 1
cur = res
while end < len(s) - 1:
while s[start] not in tmp and start < end:
start += 1
while end < len(s) - 1 and end - start + 1 < k:
end += 1
if s[end] in tmp:
cur += 1
res = max(res, cur)
if s[start] in tmp:
cur -= 1
start += 1
return res
|
思路2
保证一个长度为k的窗从左向右划即可,时间复杂度O(n)。
代码2
1
2
3
4
5
6
7
8
9
|
class Solution:
def maxVowels(self, s: str, k: int) -> int:
res, cur = 0, 0
for i in range(len(s)):
cur += s[i] in "aeiou"
if i >= k:
cur -= s[i - k] in "aeiou"
res = max(res, cur)
return res
|
二叉树中的伪回文路径
一个节点值范围在1到9的二叉树,求从其根到叶子的所有路径中的伪回文路径个数。
其中伪回文路径指的是路径中的数字可以排列成回文序列。
示例
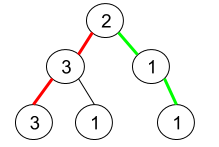
输入:root = [2,3,1,3,1,null,1]
输出:2
解释:上图为给定的二叉树。总共有 3 条从根到叶子的路径:红色路径 [2,3,3] ,绿色路径 [2,1,1] 和路径 [2,3,1] 。在这些路径中,只有红色和绿色的路径是伪回文路径,因为红色路径 [2,3,3] 存在回文排列 [3,2,3] ,绿色路径 [2,1,1] 存在回文排列 [1,2,1] 。
思路
DFS。
首先,能够排列成回文序列的条件有两种:
1、所有数字都出现了偶数次
2、只有一个数字出现了奇数次
所以用一个数组path记录每个数字出现的奇偶次数,出现奇数次则记为1,出现偶数次则记为0,所以dfs到叶节点后对path求和,和值小于等于1则表示该路径为一个伪回文路径。
因为dfs传递的path是传引用,所以每次递归前都要拷贝一次path以免影响其它路径下的path,所以空间复杂度大概会比较高。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pseudoPalindromicPaths (self, root: TreeNode) -> int:
self.res = 0
def dfs(node, path):
tmp = []
tmp[:] = path
if not node.left and not node.right:
if tmp[node.val] == 1:
tmp[node.val] = 0
else:
tmp[node.val] = 1
if sum(tmp) <= 1:
self.res += 1
return
if tmp[node.val] == 1:
tmp[node.val] = 0
else:
tmp[node.val] = 1
if node.left:
dfs(node.left, tmp)
if node.right:
dfs(node.right, tmp)
dfs(root, [0 for i in range(10)])
return self.res
|
思路2
DFS+回溯。
用一个集合记录出现奇数次的数,当访问到叶节点后判断该集合的长度是否≤1即可。
要注意每次需要将集合状态回溯到访问当前节点前的状态,避免影响其它递归路径。
代码2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution:
def pseudoPalindromicPaths (self, root: TreeNode) -> int:
tmp = set() # 记录出现奇数次的数
def dfs(node):
if not node:
return 0
if node.val in tmp:
tmp.discard(node.val)
else:
tmp.add(node.val)
res = dfs(node.left) + dfs(node.right)
if not node.left and not node.right:
res += len(tmp) <= 1
# 将集合恢复为访问该节点前的状态,避免影响其它递归路径,相当于回溯
if node.val in tmp:
tmp.discard(node.val)
else:
tmp.add(node.val)
return res
return dfs(root)
|
两个子序列的最大点积
给你两个数组 nums1 和 nums2 。
请你返回 nums1 和 nums2 中两个长度相同的 非空 子序列的最大点积。
数组的非空子序列是通过删除原数组中某些元素(可能一个也不删除)后剩余数字组成的序列,但不能改变数字间相对顺序。比方说,[2,3,5] 是 [1,2,3,4,5] 的一个子序列而 [1,5,3] 不是。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/max-dot-product-of-two-subsequences
示例
输入:nums1 = [2,1,-2,5], nums2 = [3,0,-6]
输出:18
解释:从 nums1 中得到子序列 [2,-2] ,从 nums2 中得到子序列 [3,-6] 。它们的点积为 (23 + (-2)(-6)) = 18 。
输入:nums1 = [3,-2], nums2 = [2,-6,7]
输出:21
解释:从 nums1 中得到子序列 [3] ,从 nums2 中得到子序列 [7] 。它们的点积为 (3*7) = 21 。
输入:nums1 = [-1,-1], nums2 = [1,1]
输出:-1
解释:从 nums1 中得到子序列 [-1] ,从 nums2 中得到子序列 [1] 。它们的点积为 -1 。
思路
DP。
dp[i][j]表示从nums1中的前i个数和nums2中的前j个数中可以得到的最大点积。
有5种选择子序列的可能:
1、只选择nums1第i个数和nums2第j个数的乘积作为点积,这一步也相当于对dp[i][j]初始化,即dp[i][j] = nums1[i-1][j-1]
2、不选择nums1第i个数和nums2第j个数,即dp[i-1][j-1]
3、nums1第i个数和nums2第j个数都选择进来,即dp[i-1][j-1]+nums1[i-1]*nums2[j-1]
4、只选择nums1的第i个数,不选择nums2的第j个数,即dp[i][j-1]
5、只选择nums2的第j个数,不选择nums1的第i个数,即dp[i-1][j]
选择上述选择中的最大值作为最终dp[i][j]的值。
代码
1
2
3
4
5
6
7
8
9
|
class Solution:
def maxDotProduct(self, nums1: List[int], nums2: List[int]) -> int:
n, m = len(nums1), len(nums2)
dp = [[-1001] * (m + 1) for i in range(n + 1)]
for i in range(1, n+1):
for j in range(1, m+1):
dp[i][j] = nums1[i-1] * nums2[j-1]
dp[i][j] = max(dp[i][j], dp[i-1][j-1], dp[i-1][j-1] + dp[i][j], dp[i-1][j], dp[i][j-1])
return dp[n][m]
|
总结
仅AC前三题
得分12/18,完成时间0:47:29,排名 916/3350
1、第一题刚开始用in来找前缀,显然是错的,因为in找的是searchWord是否包含在单词内,是非前缀的,用时0:06:01,被罚时1次
2、第二题把问题想复杂了,用了双指针(其实只需要保持一个长度为k的窗从左往右划即可,因为长的窗包含的元音个数肯定要大于等于相同范围内的短窗),导致边界问题变得复杂,过用例过了挺久,用时0:25:25
3、第三题DFS,比较熟了,比第二题用时要少一些,用时0:42:29
4、第四题要用DP,想了18分钟,没思路,放弃。
文章作者
Single Long
上次更新
2020-07-31
(6e089dc)
Update Leetcode reviews
许可协议
CC BY-NC-ND 4.0
