目录
数组中两元素的最大乘积
给你一个整数数组 nums,请你选择数组的两个不同下标 i 和 j,使 (nums[i]-1)*(nums[j]-1) 取得最大值。
请你计算并返回该式的最大值。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-product-of-two-elements-in-an-array
示例
输入:nums = [3,4,5,2]
输出:12
解释:如果选择下标 i=1 和 j=2(下标从 0 开始),则可以获得最大值,(nums[1]-1)(nums[2]-1) = (4-1)(5-1) = 3*4 = 12 。
思路1
排序,然后取最大和次大的数。O(nlogn)
代码1
1
2
3
4
|
class Solution:
def maxProduct(self, nums: List[int]) -> int:
nums.sort()
return (nums[-1] - 1) * (nums[-2] - 1)
|
思路2
一次循环遍历即可选出最大和次大的数。O(n)
代码2
1
2
3
4
5
6
7
8
9
|
class Solution:
def maxProduct(self, nums: List[int]) -> int:
fst, sec = 1, 1
for num in nums:
if num > fst:
fst, sec = num, fst
elif num > sec:
sec = num
return (fst-1)*(sec-1)
|
切割后面积最大的蛋糕
矩形蛋糕的高度为 h 且宽度为 w,给你两个整数数组 horizontalCuts 和 verticalCuts,其中 horizontalCuts[i] 是从矩形蛋糕顶部到第 i 个水平切口的距离,类似地, verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口的距离。
请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后,请你找出 面积最大 的那份蛋糕,并返回其 面积 。由于答案可能是一个很大的数字,因此需要将结果对 10^9 + 7 取余后返回。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-area-of-a-piece-of-cake-after-horizontal-and-vertical-cuts
示例
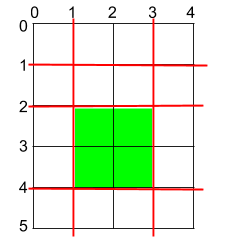
输入:h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
输出:4
解释:上图所示的矩阵蛋糕中,红色线表示水平和竖直方向上的切口。切割蛋糕后,绿色的那份蛋糕面积最大。
思路1
分别求水平切和竖直切间隔最大的两切间隔,然后做乘法即可。
需要先对两种切法进行排序。O(nlogn)
代码1
1
2
3
4
5
6
7
8
9
10
11
|
class Solution:
def maxArea(self, h: int, w: int, horizontalCuts: List[int], verticalCuts: List[int]) -> int:
ho = [0] + sorted(horizontalCuts) + [h]
ve = [0] + sorted(verticalCuts) + [w]
hmax, vmax = 0, 0
m = 10**9 + 7
for i in range(1, len(ho)):
hmax = max(hmax, ho[i]-ho[i-1]) % m
for i in range(1, len(ve)):
vmax = max(vmax, ve[i]-ve[i-1]) % m
return (hmax * vmax) % m
|
重新规划路线
n 座城市,从 0 到 n-1 编号,其间共有 n-1 条路线。因此,要想在两座不同城市之间旅行只有唯一一条路线可供选择(路线网形成一颗树)。去年,交通运输部决定重新规划路线,以改变交通拥堵的状况。
路线用 connections 表示,其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。
今年,城市 0 将会举办一场大型比赛,很多游客都想前往城市 0 。
请你帮助重新规划路线方向,使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。
题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/reorder-routes-to-make-all-paths-lead-to-the-city-zero
示例
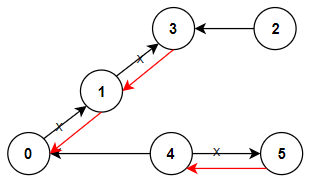
输入:n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
输出:3
解释:更改以红色显示的路线的方向,使每个城市都可以到达城市 0 。
思路1
原先用一个数组保存可达0的节点,然后每次要用O(n)查找当前节点是否在可达0的数组内,这样需要O(n^2),就超时了。
之后用了记忆化搜索,空间换时间。即用dp[i]表示第i个节点是否可达0,可达为1,否则为0。当当前路径的目的节点可达0时,则源节点也将可达0,设dp[源节点]等于1即可;若当前节点的源节点可达0时,说明需要改变路径的方向,res加1,路径方向改变后,原来的目的节点变为源节点,变得可达0,即dp[目的节点]等于1。一次遍历O(n)。
这个方法默认测试用例是按从0开始由近及远的顺序铺开的,结果真的通过了。
代码1
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution:
def minReorder(self, n: int, connections: List[List[int]]) -> int:
dp = [0 for i in range(n)]
dp[0] = 1
res = 0
for conn in connections:
if dp[conn[1]]:
dp[conn[0]] = 1
continue
if dp[conn[0]]:
res += 1
dp[conn[1]] = 1
return res
|
思路2
把有向无环图看做一棵树,用DFS遍历。
用一个邻接表记录每个源节点相邻的节点,正表示是从源节点出发到达的节点,负表示是进入到源节点的节点。因为是从根节点0出发遍历,因此正表示的是父节点出发到子节点,则此时子节点无法达到0节点,需要转向。
需要遍历每一个节点,O(n)
代码2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution:
def minReorder(self, n, connections):
def dfs(al, visited, source):
change = 0
visited[source] = True
for to in al[source]:
if not visited[abs(to)]:
if to > 0:
# 出节点表示方向不对,需要转向
change += dfs(al, visited, abs(to)) + 1
else:
# 入节点,继续往下递归
change += dfs(al, visited, abs(to))
return change
al = [[] for _ in range(n)]
visited = [False for _ in range(n)] # 记录节点是否被访问
for conn in connections:
al[conn[0]].append(conn[1]) # 正表示出节点
al[conn[1]].append(-conn[0]) # 负表示入节点
return dfs(al, visited, 0) # 从根0往下遍历
|
两个盒子中球的颜色数相同的概率
桌面上有 2n 个颜色不完全相同的球,球上的颜色共有 k 种。给你一个大小为 k 的整数数组 balls ,其中 balls[i] 是颜色为 i 的球的数量。
所有的球都已经 随机打乱顺序 ,前 n 个球放入第一个盒子,后 n 个球放入另一个盒子。
注意:这两个盒子是不同的。例如,两个球颜色分别为 a 和 b,若盒子分别为 [] 和 (),那么 [a] (b) 和 [b] (a) 这两种分配方式是不同的。
请计算「两个盒子中球的颜色数相同」的情况的概率。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/probability-of-a-two-boxes-having-the-same-number-of-distinct-balls
示例
输入:balls = [2,1,1]
输出:0.66667
解释:球的列表为 [1, 1, 2, 3]
随机打乱,得到 12 种等概率的不同打乱方案,每种方案概率为 1/12 :
[1,1 / 2,3], [1,1 / 3,2], [1,2 / 1,3], [1,2 / 3,1], [1,3 / 1,2], [1,3 / 2,1], [2,1 / 1,3], [2,1 / 3,1], [2,3 / 1,1], [3,1 / 1,2], [3,1 / 2,1], [3,2 / 1,1]
然后,我们将前两个球放入第一个盒子,后两个球放入第二个盒子。
这 12 种可能的随机打乱方式中的 8 种满足「两个盒子中球的颜色数相同」。
概率 = 8/12 = 0.66667
思路1
DFS+回溯。
统计满足两盒平分球的所有可能数self.all,然后统计满足[两盒中球颜色数相同]条件的数量self.good。最后做除法得概率。
参考自:https://leetcode.com/problems/probability-of-a-two-boxes-having-the-same-number-of-distinct-balls/discuss/661723/Struggling-with-probability-problems-Read-this
代码1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
class Solution:
def getProbability(self, balls: List[int]) -> float:
from math import factorial
firstHalf = {}
secondHalf = {}
self.good = 0 # 满足条件的组合数
self.all = 0 # 所有两盒平分球的组合数
def dfs(i):
if i == len(balls):
s1 = sum(firstHalf.values())
s2 = sum(secondHalf.values())
if s1 != s2:
return 0 # 两盒球数不相同,无效组合
# 求第1个盒中的组合数p1:
# 比如盒中有6个球,2个白球,2个黑球,1个红球,1个黄球
# 白球从6个位置里选2个的组合数为:C(2,6)
# 黑球从剩下4个位置里选2个:C(2,4)
# 红球从剩下2个位置里选1个:C(1,2)
# 黄球从剩下1个位置里选1个:C(1,1)
# 总的组合数 = C(2,6)*C(2,4)*C(1,2)*C(1,1) = 6! / (2!*2!*1!*1!)
prod1 = 1
for k in firstHalf:
prod1 *= factorial(firstHalf[k])
p1 = factorial(s1) / prod1
# 同理,求第2个盒中的组合数p2
prod2 = 1
for k in secondHalf:
prod2 *= factorial(secondHalf[k])
p2 = factorial(s2) / prod2
# 求出总的组合数
self.all += p1 * p2
# 求出两盒颜色数相同的组合数,很巧妙
self.good += p1 * p2 if len(firstHalf) == len(secondHalf) else 0
else:
# DFS+回溯计算颜色i的不同组合
# 例如,有3个球是颜色i时,按如下顺序进行组合:
# 0 -> 第1盒: 3个球, 第2盒: 0个球
# 1 -> 第1盒: 2个球, 第2盒: 1个球
# 2 -> 第1盒: 1个球, 第2盒: 2个球
# 3 -> 第1盒: 0个球, 第2盒: 3个球
firstHalf[i] = balls[i]
for _ in range(((balls[i])) + 1):
dfs(i + 1)
if i in firstHalf:
firstHalf[i] -= 1
if firstHalf[i] == 0:
del firstHalf[i] # 回溯
secondHalf[i] = secondHalf.get(i, 0) + 1
del secondHalf[i] # 回溯
dfs(0)
return self.good / self.all
|
总结
仅AC前三题
得分12/19,完成时间0:48:08,排名 437/3686
1、06:34,刚开始力扣卡得进不去,耽误了一些时间。题很简单,没啥好说的。
2、13:24,WA了1次,思路很清晰,代码写得很快,就是return答案时忘考虑取模被WA了1次。
3、38:08,WA了1次,刚开始用数组保存可达0的节点,需要用in来做O(n)的搜索,最后O(n^2)超时被WA了1次。然后想到用记忆化搜索,即用0和1的状态来表示是否可达,使时间复杂度减为O(n)。
4、排列组合概率题,想了22分钟,没思路,放弃。
文章作者
Single Long
上次更新
2020-07-31
(6e089dc)
Update Leetcode reviews
许可协议
CC BY-NC-ND 4.0

