目录

一维数组的动态和

给你一个数组 nums 。数组「动态和」的计算公式为：runningSum[i] = sum(nums[0]…nums[i]) 。
请返回 nums 的动态和。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/running-sum-of-1d-array

示例

输入：nums = [1,2,3,4]
输出：[1,3,6,10]
解释：动态和计算过程为 [1, 1+2, 1+2+3, 1+2+3+4] 。

思路1

用Python对nums做切片，每次都对切片求和。切片长度从1到n，故时间复杂度为O($\sum\limits_{i=1}^{n}{i}$) = O(n^2)。

代码1

1
2
3

class Solution:
    def runningSum(self, nums: List[int]) -> List[int]:
        return [sum(nums[:i]) for i in range(1, len(nums)+1)]

思路2

这题其实是前缀和，从i=1开始，nums[i-1]记录前i-1个数的和，则nums[i]加上nums[i-1]可以得到前i个数的和。一次遍历，时间复杂度O(n)。

代码2

1
2
3
4
5

class Solution:
    def runningSum(self, nums: List[int]) -> List[int]:
        for i in range(1, len(nums)):
            nums[i] += nums[i-1]
        return nums

不同整数的最少数目

给你一个整数数组 arr 和一个整数 k 。现需要从数组中恰好移除 k 个元素，请找出移除后数组中不同整数的最少数目。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/least-number-of-unique-integers-after-k-removals

示例

输入：arr = [4,3,1,1,3,3,2], k = 3
输出：2
解释：先移除 4、2 ，然后再移除两个 1 中的任意 1 个或者三个 3 中的任意 1 个，最后剩下 1 和 3 两种整数。

思路1

（超时）用count()函数统计每个数出现的次数，这里时间复杂度最高，为O(n^2)。然后按出现次数对数排序，去掉次数较少的数，更新可去掉数的个数k，当k小于等于0时，统计剩下的数的个数即为答案。

代码1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

class Solution:
    def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:
        tmp = set(arr)
        cnt = []
        for num in tmp:
            cnt.append((num, arr.count(num)))
        cnt.sort(key=lambda x:-x[1])
        while k > 0:
            cur = cnt.pop()[1]
            k -= cur
        return len(cnt) if k==0 else len(cnt)+1

思路2

（超时）代替思路1中的count()函数，用哈希表记录每个数的出现次数，时间复杂度降为O(n)。然后按出现次数对数排序，去掉次数较少的数，更新可去掉数的个数k，当k小于等于0时，统计剩下的数的个数即为答案。

这里注意最后k小于0表示最后去掉的数还有剩余个数，故保留此数，即len(cnt)+1。

代码2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

import collections

class Solution:
    def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:
        if len(arr) <= k:
            return 0     
        tmp = collections.defaultdict(int)
        for num in arr:
            tmp[num] += 1
        cnt = sorted(tmp.items(), key=lambda x:-x[1])
        while k > 0:
            cur = cnt.pop()[1]
            k -= cur
        return len(cnt) if k==0 else len(cnt)+1

制作m束花所需的最少天数

给你一个整数数组 bloomDay，以及两个整数 m 和 k 。
现需要制作 m 束花。制作花束时，需要使用花园中 相邻的 k 朵花 。
花园中有 n 朵花，第 i 朵花会在 bloomDay[i] 时盛开，恰好 可以用于 一束 花中。
请你返回从花园中摘 m 束花需要等待的最少的天数。如果不能摘到 m 束花则返回 -1 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-number-of-days-to-make-m-bouquets

示例

输入：bloomDay = [7,7,7,7,12,7,7], m = 2, k = 3
输出：12
解释：
让我们一起观察这12天的花开过程，x 表示花开，而 _ 表示花还未开。
要制作 2 束花，每束需要 3 朵。
花园在 7 天后和 12 天后的情况如下：
7 天后：[x, x, x, x, _, x, x]
可以用前 3 朵盛开的花制作第一束花。但不能使用后 3 朵盛开的花，因为它们不相邻。
12 天后：[x, x, x, x, x, x, x]
显然，我们可以用不同的方式制作两束花。

思路1

当最快第i天可以做m束花时，第i+1天必然也可以做m束花，而第i-1天做不了m束花，这里是一个隐藏的递增的关系，那么应该想到用二分查找来找这个边界值i。如果第mid天无法做成m束花，则表示只有在[mid+1, right]天内才有可能做成m束花；若第mid天可以做成m束花，则需要在[left, mid-1]天内找边界值i，但是mid也可能恰好就是边界值，在[left, mid-1]天内无法再完成m束花，因此用一个res来记录最近的可以完成m束花的mid值。

代码1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class Solution:
    def minDays(self, bloomDay: List[int], m: int, k: int) -> int:
        n = len(bloomDay)
        left, right = 1, 1000000000
        res = -1
        while left <= right:
            mid = (left + right) // 2
            cnt = 0 # 做成花束的数量
            cons = 0 # 相邻开花的数量
            for i in range(n):
                if bloomDay[i] <= mid:
                    cons += 1
                    if cons == k:
                        cnt += 1
                        cons = 0
                else:
                    cons = 0
            if cnt >= m:
                res = mid
                right = mid - 1
            else:
                left = mid + 1
        return res

树节点的第k个祖先

给你一棵树，树上有 n 个节点，按从 0 到 n-1 编号。树以父节点数组的形式给出，其中 parent[i] 是节点 i 的父节点。树的根节点是编号为 0 的节点。

请你设计并实现 getKthAncestor(int node, int k) 函数，函数返回节点 node 的第 k 个祖先节点。如果不存在这样的祖先节点，返回 -1 。

树节点的第 k 个祖先节点是从该节点到根节点路径上的第 k 个节点。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/kth-ancestor-of-a-tree-node

示例

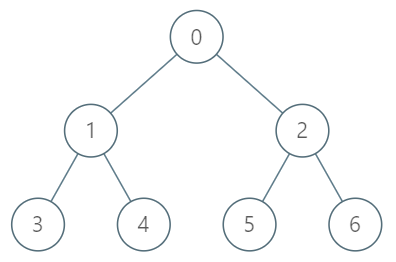
输入：
[“TreeAncestor”,“getKthAncestor”,“getKthAncestor”,“getKthAncestor”]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]
输出：
[null,1,0,-1]
解释：
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);
treeAncestor.getKthAncestor(3, 1); // 返回 1 ，它是 3 的父节点
treeAncestor.getKthAncestor(5, 2); // 返回 0 ，它是 5 的祖父节点
treeAncestor.getKthAncestor(6, 3); // 返回 -1 因为不存在满足要求的祖先节点

思路1

(超时)parent[node]记录的本身是节点node的父节点索引，因此用 node = parent[node] 不断循环至多k次或到node等于-1时，即可找到node的k级祖先。但是当树退化为链表时，由题目给的限制，树高可以达到n = 5*10^4，而查询次数至多也是m = 5*10^4次，因此时间复杂度O(nm)超时。

代码1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class TreeAncestor:

    def __init__(self, n: int, parent: List[int]):
        self.n = n
        self.parent = parent

    def getKthAncestor(self, node: int, k: int) -> int:
        while k > 0 and node != -1:
            node = self.parent[node]
            k -= 1
        return node

# Your TreeAncestor object will be instantiated and called as such:
# obj = TreeAncestor(n, parent)
# param_1 = obj.getKthAncestor(node,k)

思路2

参考自：https://leetcode-cn.com/problems/kth-ancestor-of-a-tree-node/solution/li-kou-zai-zhu-jian-ba-acm-mo-ban-ti-ban-shang-lai/

这里用的是ACM中常用的LCA倍增查询模板，其实可以理解为一种记忆化搜索。
在二叉树中，有这样一个递推关系：与第i个节点距离为2^(j-1)的祖先与第i个节点距离为2^j的祖先的距离为2^(j-1)。
用dp[i][j]记录parent中与第i个节点距离2^j的祖先，则有递推式dp[i][j] = dp[dp[i][j-1]][j-1],由此可以用dp二维数组记忆所有节点的所有祖先。

查询K级祖先的没看太懂。

代码2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

class TreeAncestor:

    def __init__(self, n: int, parent: List[int]):
        self.dp = [] # dp[i][j]存储第i个节点距离为2^j的祖先
        for i in range(n):
            self.dp.append([parent[i]])
        j = 1
        # 这种解法比较节约空间，因为刚开始并不知道j可以到几层
        # 此解法可以得到最小可满足要求的j
        while True:
            flag = True # 是否此次循环2^j距离已大于所有节点与树根节点的距离
            for i in range(n):
                tmp = self.dp[self.dp[i][j-1]][j-1] if self.dp[i][j-1] != -1 else -1
                self.dp[i].append(tmp)
                if tmp != -1:
                    flag = False
            if flag:
                break
            j += 1

    def getKthAncestor(self, node: int, k: int) -> int:
        res = node
        pos = 0
        while k and res != -1:
            if pos >= len(self.dp[res]):
                return -1
            if k & 1:
                res = self.dp[res][pos]
            pos += 1
            k >>= 1
        return res

# Your TreeAncestor object will be instantiated and called as such:
# obj = TreeAncestor(n, parent)
# param_1 = obj.getKthAncestor(node,k)

总结

仅AC前两题
得分7/18，完成时间0:24:47，全国排名 1319/3803，全球排名 5159/13794。
1、01:36，直接暴力了，没想到前缀和，太菜。
2、19:47，超时了1次，然后用哈希表空间换时间搞定。
3、菜鸟是想不到这题居然是用二分查找的。
4、ACM的模板题，别人分分钟写出来的题，菜鸟看了一天题解也还没完全看懂。
目前全国排名2120，全球排名10768。