目录
去掉最低工资和最高工资后的工资平均值
给你一个整数数组 salary ,数组里每个数都是 唯一 的,其中 salary[i] 是第 i 个员工的工资。
请你返回去掉最低工资和最高工资以后,剩下员工工资的平均值。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/average-salary-excluding-the-minimum-and-maximum-salary
示例
输入:salary = [4000,3000,1000,2000]
输出:2500.00000
解释:最低工资和最高工资分别是 1000 和 4000 。
去掉最低工资和最高工资以后的平均工资是 (2000+3000) / 2 = 2500
思路1
排序O(nlogn),pop掉最后一个最大的O(1),pop掉第一个最小的O(n),求剩下的平均值。总时间复杂度O(nlogn)。
代码1
1
2
3
4
5
6
|
class Solution:
def average(self, salary: List[int]) -> float:
salary.sort()
salary.pop()
salary.pop(0)
return sum(salary) / len(salary)
|
n的第k个因子
给你两个正整数 n 和 k 。
如果正整数 i 满足 n % i == 0 ,那么我们就说正整数 i 是整数 n 的因子。
考虑整数 n 的所有因子,将它们 升序排列 。请你返回第 k 个因子。如果 n 的因子数少于 k ,请你返回 -1 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/the-kth-factor-of-n
示例
输入:n = 12, k = 3
输出:3
解释:因子列表包括 [1, 2, 3, 4, 6, 12],第 3 个因子是 3 。
思路1
暴力枚举O(n),到第k个可整除n的数就返回该数,否则返回-1
代码1
1
2
3
4
5
6
7
8
9
|
class Solution:
def kthFactor(self, n: int, k: int) -> int:
cnt = 0
for i in range(1, n+1):
if n % i == 0:
cnt += 1
if cnt == k:
return i
return -1
|
删掉一个元素以后全为1的最长子数组
给你一个二进制数组 nums ,你需要从中删掉一个元素。
请你在删掉元素的结果数组中,返回最长的且只包含 1 的非空子数组的长度。
如果不存在这样的子数组,请返回 0 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/longest-subarray-of-1s-after-deleting-one-element
示例
输入:nums = [1,1,0,1]
输出:3
解释:删掉位置 2 的数后,[1,1,1] 包含 3 个 1 。
思路1
遍历一次nums,用两个数组分别记录每段0和1的个数。记录1的个数的数组ones为空时,返回0;记录0的个数的数组zeros为空时,表示nums全为1,返回nums的长度减1;ones的长度为1时表示只有一段1,返回该段长度。
zeros和ones都非空时。若nums第一段为0段,此段对结果无影响,去掉该0段。遍历zeros,遇到长度为1的0段时,加上对应ones中的前后两个1段,更新res。
代码1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
class Solution:
def longestSubarray(self, nums: List[int]) -> int:
ones = []
zeros = []
onec, zc = 0, 0
for num in nums:
if num == 0:
if onec != 0:
ones.append(onec)
onec = 0
zc += 1
else:
if zc != 0:
zeros.append(zc)
zc = 0
onec += 1
if onec != 0:
ones.append(onec)
if zc != 0:
zeros.append(zc)
if not ones:
return 0
if not zeros:
return len(nums) - 1
if len(ones) == 1:
return ones[0]
if nums[0] == 0:
zeros.pop(0)
res = 0
for i in range(len(zeros)):
if zeros[i] == 1:
try:
res = max(res, ones[i] + ones[i+1])
except:
pass
return max(res, max(ones))
|
思路2
先从左往右遍历,记录左边连续1的个数,若第i个位置为0,则记为pre[i] = 0;
在从右往左遍历,记录右边连续1的个数,若第i个位置为0,则记为suf[i] = 0;
先处理边界问题,即位置1和位置n,res = max(suf[0]-1, pre[-1]-1);
再遍历位置1到n-1,删除第i个位置的元素可以形成的最长的连续1段长度为pre[i-1] + suf[i+1], 更新res = max(res, pre[i-1]+suf[i+1])
代码2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution:
def longestSubarray(self, nums: List[int]) -> int:
n = len(nums)
pre = [0] * n
suf = [0] * n
pre[0] = nums[0]
for i in range(1, n):
if nums[i] == 1:
pre[i] = pre[i-1] + 1
suf[-1] = nums[-1]
for i in range(n-2, -1, -1):
if nums[i] == 1:
suf[i] = suf[i+1] + 1
res = max(suf[0]-1, pre[-1]-1)
for i in range(1, n-1):
res = max(res, pre[i-1]+suf[i+1])
return res
|
并行课程II
给你一个整数 n 表示某所大学里课程的数目,编号为 1 到 n ,数组 dependencies 中, dependencies[i] = [xi, yi] 表示一个先修课的关系,也就是课程 xi 必须在课程 yi 之前上。同时你还有一个整数 k 。
在一个学期中,你 最多 可以同时上 k 门课,前提是这些课的先修课在之前的学期里已经上过了。
请你返回上完所有课最少需要多少个学期。题目保证一定存在一种上完所有课的方式。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/parallel-courses-ii
示例
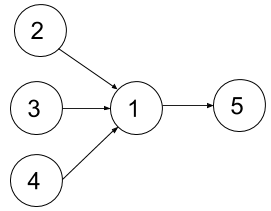
输入:n = 5, dependencies = [[2,1],[3,1],[4,1],[1,5]], k = 2
输出:4
解释:上图展示了题目输入的图。一个最优方案是:第一学期上课程 2 和 3,第二学期上课程 4 ,第三学期上课程 1 ,第四学期上课程 5 。
思路1
参考了210题【课程表II】的拓扑排序方法。用集合列表实现邻接表记录每门课的后导课程,并记录每门课的入度。入度为0的课程入队(入度为0的课表示当前学期可以学习的课程),每次循环代表一个学期,出队的个数是k和当前队列长度的最小值,且出度较多的课程先出队,增加通过用例的概率。
代码1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
class Solution:
def minNumberOfSemesters(self, n: int, dependencies: List[List[int]], k: int) -> int:
if len(dependencies) == 0:
return math.ceil(n / k)
inDegree = [0 for i in range(n)] # 入度数组
adj = [set() for _ in range(n)] # 记录每门课的后导课程的邻接表(同DFS中的graph也可以用哈希表实现)
# 先初始化邻接表和入度数组
for first, second in dependencies:
adj[first-1].add(second-1)
inDegree[second-1] += 1
queue = [] # 记录入度为0的节点
res = 0
cnt = 0
# 将入度为0的节点,即没有先导课程的课程入列
for i, degree in enumerate(inDegree):
if degree == 0:
queue.append(i)
level = len(queue)
while queue:
size = min(level, k)
for _ in range(size):
top = queue.pop(0)
# 以当前课程top为先导课程的课程入度减1
for course in adj[top]:
inDegree[course] -= 1
# 入度减为0时入列
if inDegree[course] == 0:
queue.append(course)
res += 1
# 贪心,把出度最多的课程先出栈
tmp = []
for q in queue:
tmp.append([q, len(adj[q])])
tmp.sort(key=lambda x:-x[1])
for i in range(len(tmp)):
queue[i] = tmp[i][0]
level = len(queue)
return res
|
总结
AC前三题
得分12/18,完成时间0:34:43,全国排名 645/2260,全球排名 2452/7933。
1、01:10,按题意模拟运算过程即可
2、03:20,数据量小,直接暴力
3、19:43,面向用例编程,WA了三次;比赛时用的思路1,即模拟过程,特殊情况较多,WA了多次;思路2使用了左右两个方向的遍历来记录1段的长度,最后再结合起来,思路比较清晰。
4、有向无环图的拓扑排序+贪心,比赛时没有想到贪心,只差一个用例未通过,错失第二次全AC的机会;题解中说正解应该是状态压缩DP,因为贪心并不能保证课程学习顺序的正确性,只是提高了通过用例的概率(所以有的人用随机化出队来碰运气)。
目前全国排名2567,全球排名12510。
文章作者
Single Long
上次更新
2020-07-31
(6e089dc)
Update Leetcode reviews
许可协议
CC BY-NC-ND 4.0
