目录
判断能否形成等差数列
给你一个数字数组 arr 。
如果一个数列中,任意相邻两项的差总等于同一个常数,那么这个数列就称为 等差数列 。
如果可以重新排列数组形成等差数列,请返回 true ;否则,返回 false 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/can-make-arithmetic-progression-from-sequence
示例
输入:arr = [3,5,1]
输出:true
解释:对数组重新排序得到 [1,3,5] 或者 [5,3,1] ,任意相邻两项的差分别为 2 或 -2 ,可以形成等差数列。
思路1
先排序,然后将相邻元素差值加入到一个集合中,如果集合中只有一种差值,说明是等差数列。
代码1
1
2
3
4
5
6
7
|
class Solution:
def canMakeArithmeticProgression(self, arr: List[int]) -> bool:
tmp = set()
arr.sort()
for i in range(1, len(arr)):
tmp.add(arr[i] - arr[i-1])
return len(tmp) == 1
|
所有蚂蚁掉下来前的最后一刻
有一块木板,长度为 n 个 单位 。一些蚂蚁在木板上移动,每只蚂蚁都以 每秒一个单位 的速度移动。其中,一部分蚂蚁向 左 移动,其他蚂蚁向 右 移动。
当两只向 不同 方向移动的蚂蚁在某个点相遇时,它们会同时改变移动方向并继续移动。假设更改方向不会花费任何额外时间。
而当蚂蚁在某一时刻 t 到达木板的一端时,它立即从木板上掉下来。
给你一个整数 n 和两个整数数组 left 以及 right 。两个数组分别标识向左或者向右移动的蚂蚁在 t = 0 时的位置。请你返回最后一只蚂蚁从木板上掉下来的时刻。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/last-moment-before-all-ants-fall-out-of-a-plank
示例
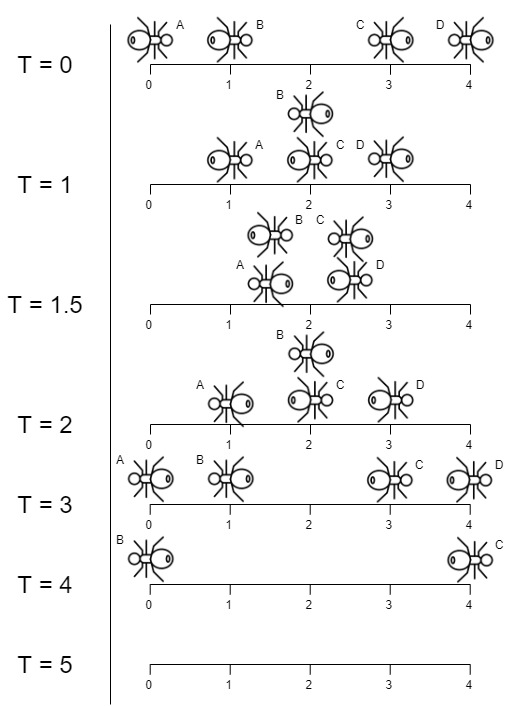
输入:n = 4, left = [4,3], right = [0,1]
输出:4
解释:如上图所示:
-下标 0 处的蚂蚁命名为 A 并向右移动。
-下标 1 处的蚂蚁命名为 B 并向右移动。
-下标 3 处的蚂蚁命名为 C 并向左移动。
-下标 4 处的蚂蚁命名为 D 并向左移动。
请注意,蚂蚁在木板上的最后时刻是 t = 4 秒,之后蚂蚁立即从木板上掉下来。(也就是说在 t = 4.0000000001 时,木板上没有蚂蚁)。
思路1
参考自:https://leetcode-cn.com/problems/last-moment-before-all-ants-fall-out-of-a-plank/solution/ma-yi-you-mei-de-pa-pa-pa-pa-by-imcover/
将蚂蚁碰撞调头看作是相互穿透(只不过蚂蚁间互换了身份)。如示例中从T=0到T=3,能看出和穿透的效果是一样的。
代码1
1
2
3
4
5
6
7
8
|
class Solution:
def getLastMoment(self, n: int, left: List[int], right: List[int]) -> int:
res = -1
for l in left:
res = max(res, l)
for r in right:
res = max(res, n - r)
return res
|
统计全1子矩形
给你一个只包含 0 和 1 的 rows * columns 矩阵 mat ,请你返回有多少个 子矩形 的元素全部都是 1 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/count-submatrices-with-all-ones
示例
输入:
mat =
[[1,0,1],
[1,1,0],
[1,1,0]]
输出:13
解释:
有 6 个 1x1 的矩形。
有 2 个 1x2 的矩形。
有 3 个 2x1 的矩形。
有 1 个 2x2 的矩形。
有 1 个 3x1 的矩形。
矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。
思路1
单调栈。感觉比较复杂,等官方答案出了再理一理吧。
代码1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution:
def numSubmat(self, mat: List[List[int]]) -> int:
m, n = len(mat), len(mat[0])
up = [[0] * n for _ in range(m)]
for i in range(m):
for j in range(n):
if mat[i][j] == 1:
up[i][j] = 1 if i == 0 else 1 + up[i-1][j]
else:
up[i][j] = 0
res = 0
for i in range(m):
stack = [(-1, 0)]
for j in range(n):
while stack[-1][0] != -1 and up[i][stack[-1][0]] >= up[i][j]:
stack.pop()
cur = up[i][j] * (j - stack[-1][0]) + stack[-1][1]
res += cur
stack.append((j, cur))
return res
|
最多K次交换相邻数位后得到的最小整数
给你一个字符串 num 和一个整数 k 。其中,num 表示一个很大的整数,字符串中的每个字符依次对应整数上的各个 数位 。
你可以交换这个整数相邻数位的数字 最多 k 次。
请你返回你能得到的最小整数,并以字符串形式返回。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits
示例
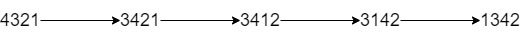
输入:num = “4321”, k = 4
输出:“1342”
解释:4321 通过 4 次交换相邻数位得到最小整数的步骤如上图所示。
思路1
暴力递归。时间复杂度O(n^2)。
代码1
1
2
3
4
5
6
7
8
9
10
11
|
class Solution:
def minInteger(self, num: str, k: int) -> str:
for i in range(10):
index = num.find(str(i))
if index < 0:
continue
if index <= k:
if k == index:
return str(i) + num[:index] + num[index+1:]
return str(i) + self.minInteger(num[:index] + num[index+1:], k - index)
return num
|
思路2
参考自:https://leetcode-cn.com/problems/minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits/solution/java-rmqfenwich-tree-onlgn-by-henrylee4/
基于一种叫Fenwich树的树状数组的数据结构的RMQ算法(区间最值查询),时间复杂度为O(nlogn)。
代码2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
|
class Solution:
class FenwichTree:
def __init__(self, nums):
self.sums = [0] * (len(nums) + 1)
self.nums = nums
for i in range(len(nums)):
self.updateBit(i + 1, nums[i])
def update(self, i, val):
self.updateBit(i + 1, val - self.nums[i])
self.nums[i] = val
def updateBit(self, i, diff):
while i < len(self.sums):
self.sums[i] += diff
i += self.lowBit(i)
def sumRange(self, i, j):
return self.preSum(j + 1) - self.preSum(i)
def preSum(self, i):
sum = 0
while i > 0:
sum += self.sums[i]
i -= self.lowBit(i)
return sum
def lowBit(self, i):
return i & -i
def minInteger(self, num: str, k: int) -> str:
# 统计0-9的所有位置
idLists = []
for _ in range(10):
idLists.append([])
n = len(num)
for i in range(n):
idLists[ord(num[i]) - ord("0")].append(i)
# 指向idLists的0-9的当前位置
ids = [0] * 10
seen = [False] * n
res = ""
# 统计范围内已被使用的下标,计算需要转换的次数时需要去掉已被转换到前面的那些下标
fwt = Solution.FenwichTree([0] * n)
ind = 0
while len(res) < n:
if seen[ind]:
# 如果已经被置换过了,跳过
ind += 1
continue
cur = ord(num[ind]) - ord("0")
# 查找比当前元素小且满足条件的最小值的下标
flag = False
for j in range(cur):
while ids[j] < len(idLists[j]) and idLists[j][ids[j]] < ind:
ids[j] += 1
if ids[j] == len(idLists[j]):
continue
index = idLists[j][ids[j]]
seenNum = fwt.sumRange(0, index - 1)
if index - seenNum <= k:
# 找到了满足条件的值,更新状态
k -= index - seenNum
ids[j] += 1
seen[index] = True
fwt.update(index, 1)
ind -= 1
res += str(j)
flag = True
break
if not flag:
# 找不到满足条件且小于当前值的值,更新状态
seen[ind] = True
fwt.update(ind, 1)
res += str(cur)
ind += 1
return res
|
总结
AC第1题和第3题。
得分8/19,完成时间1:13:54,全国排名 884/5506,全球排名 2501/14301。
1、01:23,等差数列性质,简单数学题。
2、智力题做不出来,说明智商已不在线。
3、1:13:54,依赖单调栈求子矩阵个数。
4、测试用例很弱,O(n^2)暴力可AC。正解应为基于树状数组的RMQ算法,时间复杂度为O(nlogn)。但是两种方法用Python实现的话暴力反而会比RMQ花费时间少。不过我连暴力解都写不出来,RMQ短时间内也看不懂,又被自己菜到了。
目前全国排名2567,全球排名12510。
文章作者
Single Long
上次更新
2020-07-31
(6e089dc)
Update Leetcode reviews
许可协议
CC BY-NC-ND 4.0