目录
好数对的数目
给你一个整数数组 nums 。如果一组数字 (i,j) 满足 nums[i] == nums[j] 且 i < j ,就可以认为这是一组 好数对 。返回好数对的数目。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/number-of-good-pairs
示例
输入:nums = [1,2,3,1,1,3]
输出:4
解释:有 4 组好数对,分别是 (0,3), (0,4), (3,4), (2,5) ,下标从 0 开始
思路1
双重循环,保证内循环的下标j比外循环的下标i大,当nums[i]等于nums[j]时即为一个好数对。
代码1
1
2
3
4
5
6
7
8
9
|
class Solution:
def numIdenticalPairs(self, nums: List[int]) -> int:
n = len(nums)
res = 0
for i in range(n):
for j in range(i+1, n):
if nums[i] == nums[j]:
res += 1
return res
|
仅含1的子串数
给你一个二进制字符串 s(仅由 ‘0’ 和 ‘1’ 组成的字符串)。
返回所有字符都为 1 的子字符串的数目。
由于答案可能很大,请你将它对 10^9 + 7 取模后返回。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/number-of-substrings-with-only-1s
示例
输入:s = “0110111”
输出:9
解释:共有 9 个子字符串仅由 ‘1’ 组成
“1” -> 5 次
“11” -> 3 次
“111” -> 1 次
思路1
其实是个等差数列求和,如“111111”中有6个“1”,5个“11”,4个“111”,3和“1111”,2个“11111”,1个“111111”。即其实是从1开始,到长度n结束,等差为1的等差数列求和 = n * (1 + n) / 2。所以统计出所有的1段并求它们的等差数列和即可。
代码1
1
2
3
4
5
6
7
8
9
|
class Solution:
def numSub(self, s: str) -> int:
s = s.split("0")
mod = 10**9 + 7
res = 0
for c in s:
if c:
res += len(c) * (1+len(c)) // 2 % mod
return res % mod
|
概率最大的路径
给你一个由 n 个节点(下标从 0 开始)组成的无向加权图,该图由一个描述边的列表组成,其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边,且该边遍历成功的概率为 succProb[i] 。
指定两个节点分别作为起点 start 和终点 end ,请你找出从起点到终点成功概率最大的路径,并返回其成功概率。
如果不存在从 start 到 end 的路径,请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ,就会被视作正确答案。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/path-with-maximum-probability
示例
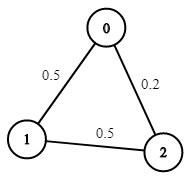
输入:n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出:0.25000
解释:从起点到终点有两条路径,其中一条的成功概率为 0.2 ,而另一条为 0.5 * 0.5 = 0.25
思路1
DFS,超时未通过,仅作日后教训用。
用哈希表做邻接表记录一个节点可以到达的下一节点及其概率,用一个visited数组记录搜索时某个节点是否已被访问过。然后DFS,在DFS中,如果一个节点已被访问过,则终止搜索;如果当前概率已小于已求出的最大概率,也终止。否则,遍历当前节点的邻接表做DFS,如果遍历过程中到达目的节点,则更新全局res的最大值。遍历结束后将该节点回溯为未访问状态避免影响其它搜索路线。
理不出DFS思路的逻辑上的问题,但是就是会陷入死循环到超时。难道是因为对无向图不好用DFS吗?
代码1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution:
def maxProbability(self, n: int, edges, succProb, start: int, end: int) -> float:
adj = collections.defaultdict(list)
for i in range(len(edges)):
adj[edges[i][0]].append([edges[i][1], succProb[i]])
adj[edges[i][1]].append([edges[i][0], succProb[i]])
def dfs(tmp, cur):
if visited[tmp] == 1:
return
if cur <= self.res:
return
visited[tmp] = 1
for t in adj[tmp]:
if t[0] == end:
self.res = max(self.res, cur * t[1])
return
dfs(t[0], cur * t[1])
visited[tmp] = 0
visited = [0] * n
self.res = 0
dfs(start, 1)
return self.res
|
思路2
BFS+记忆化搜索,通过。
同思路1一样,先做每个节点的可达节点及其到达概率的邻接表。用dp[i]记录到达节点i的最大概率。用双端队列记录有价值访问的节点,初始start节点入队。
如何定义节点是否有价值访问呢?先将队列里左端节点出队,然后遍历它的邻接表,如果当前节点cur的概率dp[cur]乘以到达邻接表的里的某个节点nxt的概率p大于当前到达nxt节点的最大概率dp[nxt]时,则说明nxt节点是有访问价值,此时用dp[cur] * p 更新 dp[nxt]并将nxt节点入队。保证有效地访问有价值节点,dp需要初始化为0,dp[start]初始化为1。这样迟早所有节点都会失去访问价值,BFS即结束。返回dp[end]即为所求。
代码2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution:
def maxProbability(self, n: int, edges, succProb, start: int, end: int) -> float:
adj = collections.defaultdict(list)
for i in range(len(edges)):
adj[edges[i][0]].append([edges[i][1], succProb[i]])
adj[edges[i][1]].append([edges[i][0], succProb[i]])
stack = collections.deque()
stack.append(start)
dp = [0 for _ in range(n)]
dp[start] = 1
while stack:
cur = stack.popleft()
for nxt, p in adj[cur]:
if dp[nxt] < dp[cur] * p:
dp[nxt] = dp[cur] * p
stack.append(nxt)
return dp[end]
|
服务中心的最佳位置
一家快递公司希望在新城市建立新的服务中心。公司统计了该城市所有客户在二维地图上的坐标,并希望能够以此为依据为新的服务中心选址:使服务中心 到所有客户的欧几里得距离的总和最小 。
给你一个数组 positions ,其中 positions[i] = [xi, yi] 表示第 i 个客户在二维地图上的位置,返回到所有客户的 欧几里得距离的最小总和 。
换句话说,请你为服务中心选址,该位置的坐标 [xcentre, ycentre] 需要使下面的公式取到最小值:
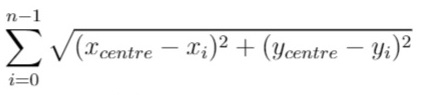
与真实值误差在 10^-5 之内的答案将被视作正确答案。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/best-position-for-a-service-centre
示例
输入:positions = [[1,1],[0,0],[2,0]]
输出:2.73205
解释:乍一看,你可能会将中心定在 [1, 0] 并期待能够得到最小总和,但是如果选址在 [1, 0] 距离总和为 3
如果将位置选在 [1.0, 0.5773502711] ,距离总和将会变为 2.73205
当心精度问题!
思路1
平均值求类心,解答错误不通过,仅作日后教训用。
Kmeans计算类心的思路,即取各轴平均值作为类心在该轴上的坐标。如果这样能通过的话就对不起这道题困难的难度了。
代码1
1
2
3
4
5
6
7
8
9
10
11
|
class Solution:
def getMinDistSum(self, positions: List[List[int]]) -> float:
n = len(positions)
x = sum(x[0] for x in positions) / n
y = sum(x[1] for x in positions) / n
res = 0
for pos in positions:
dx = pos[0] - x
dy = pos[1] - y
res += math.sqrt(dx*dx + dy*dy)
return res
|
思路2
参考自:https://www.bilibili.com/video/BV1RK4y1s79d
用退火模拟算法迭代优化逼近费马点。
Cpp的代码可以通过,改成Python后似乎会落入局部最优点出不来,暂时没Debug出来。
代码2
Cpp版本(通过):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
#define eps 1e-8
struct Point {
int x, y;
};
vector <Point> g;
double myrand() {
long long a = rand();
long long b = rand();
a = a * b % 200000 - 100000;
return ((double) a / 10);
}
double fuc(double x,double y,int n) {
double sum = 0;
for (int i = 0; i < n; i++)
sum += sqrt((x - g[i].x) * (x - g[i].x) + (y - g[i].y) * (y - g[i].y));
return sum;
}
double cold(int n) {
double tx = 0, ty = 0;
double K = 1;
double min = fuc(tx, ty, n);
while (K > eps) {
double xx, yy;
xx = myrand() * K + tx;
yy = myrand() * K + ty;
double tmp = fuc(xx, yy, n);
if (tmp < min) {
min = tmp;
tx = xx;
ty = yy;
}
K *= 0.99;
}
return min;
}
class Solution {
public:
double getMinDistSum(vector<vector<int>>& pos) {
int n = pos.size();
if (n == 1) {
return 0;
}
g.clear();
for (int i = 0; i < n; i++) {
Point now;
now.x = pos[i][0];
now.y = pos[i][1];
g.push_back(now);
}
double ans = fuc(g[0].x, g[0].y, n);
for (int i = 1; i < n; i++) {
ans = min(ans, fuc(g[i].x, g[i].y, n));
}
return min(ans, cold(n));
}
};
|
Python版本(未通过):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
class Solution:
def getMinDistSum(self, pos: List[List[int]]) -> float:
self.eps = 1e-8
def dist(x, y, n):
sum = 0
for i in range(n):
dx = pos[i][0] - x
dy = pos[i][1] - x
sum += math.sqrt(dx*dx + dy*dy)
return sum
def myrand():
a = random.randint(1, 32767)
b = random.randint(1, 32767)
a = a * b % 200000 - 100000
return float(a) / 10
def cold(n):
tx, ty = 0, 0
k = 1
res = dist(tx, ty, n)
while k > self.eps:
xx = myrand() * k + tx
yy = myrand() * k + ty
tmp = dist(xx, yy, n)
if tmp < res:
res = tmp
tx = xx
ty = yy
k *= 0.99
print(str(tx) + " " + str(ty))
return res
n = len(pos)
if n == 1:
return 0
res = dist(pos[0][0], pos[0][1], n)
for i in range(1, n):
res = min(res, dist(pos[i][0], pos[i][1], n))
return min(res, cold(n))
|
总结
仅AC前两题。
目前全国排名 2424 ,全球排名 11421 。
得分 7 / 19 ,未完成,全国排名 897 / 5273 。
1、0:01:11,依然是简单的模拟题,有思路后拼手速。
2、0:06:11,WA了1次,表面是字符串题,实际上是简单的数学题,看出是等差数列求和就很简单了,不过又忘了取模导致被WA了1次。
3、未完成,BFS加记忆化搜索可AC,比赛时用DFS做,超时,纠结于找出DFS中的逻辑错误,但是找不出来。
4、未完成。机器学习题,需要用优化方法迭代逼近解,这里是求n个点的费马点,参考视频中也是经过百度来搜索解法,但是别人搜几下就能了解到这是一个求费马点的问题,我却不能办到。参考视频采用的迭代方法是退火模拟算法。