目录

换酒问题

小区便利店正在促销，用 numExchange 个空酒瓶可以兑换一瓶新酒。你购入了 numBottles 瓶酒。

如果喝掉了酒瓶中的酒，那么酒瓶就会变成空的。

请你计算 最多 能喝到多少瓶酒。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/water-bottles

示例

输入：numBottles = 9, numExchange = 3
输出：13
解释：先喝了9瓶，再用9个空瓶换3瓶，再用3个空瓶换1瓶，共喝了9+3+1=13瓶

思路1

每次循环，记录上轮空瓶数，然后用来得到当前轮可换酒数，最后用【上轮换新酒后剩余的空瓶数】加上【这轮换来的酒喝光后得到的空瓶数】来更新当前轮得到的新空瓶数。

代码1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class Solution:
    def numWaterBottles(self, a: int, b: int) -> int:
        res = a
        ret = 0
        while a >= b:
            tmp = a # 记录上轮空瓶数
            a = a // b # 上轮空瓶当前轮可换酒数
            res += a
            a = tmp % b + a # 更新当前轮新得到的空瓶数
        return res

子树中标签相同的节点数

给你一棵树（即，一个连通的无环无向图），这棵树由编号从 0  到 n - 1 的 n 个节点组成，且恰好有 n - 1 条 edges 。树的根节点为节点 0 ，树上的每一个节点都有一个标签，也就是字符串 labels 中的一个小写字符（编号为 i 的 节点的标签就是 labels[i] ）

边数组 edges 以 edges[i] = [ai, bi] 的形式给出，该格式表示节点 ai 和 bi 之间存在一条边。

返回一个大小为 n 的数组，其中 ans[i] 表示第 i 个节点的子树中与节点 i 标签相同的节点数。

树 T 中的子树是由 T 中的某个节点及其所有后代节点组成的树。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-nodes-in-the-sub-tree-with-the-same-label

示例

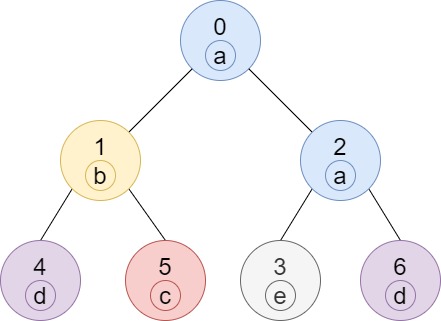
输入：n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = “abaedcd”
输出：[2,1,1,1,1,1,1]
解释：节点 0 的标签为 ‘a’ ，以 ‘a’ 为根节点的子树中，节点 2 的标签也是 ‘a’ ，因此答案为 2 。注意树中的每个节点都是这棵子树的一部分。
节点 1 的标签为 ‘b’ ，节点 1 的子树包含节点 1、4 和 5，但是节点 4、5 的标签与节点 1 不同，故而答案为 1（即，该节点本身）。

思路1

先做邻接表，用一个集合记录节点是否已有父节点，如果有父节点，则当前节点只能在邻接表中做子节点。再按从0到n-1的节点索引顺序对邻接表做BFS，超时，仅通过用例 57 / 59。

代码1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

class Solution:
    def countSubTrees(self, n: int, edges, labels):
        adj = collections.defaultdict(list)
        hasroot = set()
        for i in range(len(edges)):
            if edges[i][1] == 0:
                adj[edges[i][1]].append(edges[i][0])
                hasroot.add(edges[i][0])
                continue
            if edges[i][1] not in hasroot:
                adj[edges[i][0]].append(edges[i][1])
                hasroot.add(edges[i][1])
            else:
                adj[edges[i][1]].append(edges[i][0])
                hasroot.add(edges[i][0])

        def bfs(ind):
            label = labels[ind]
            queue = collections.deque(adj[ind])
            cur = len(queue)
            while queue:
                for _ in range(cur):
                    node = queue.popleft()
                    for nxt in adj[node]:
                        queue.append(nxt)
                    if labels[node] == label:
                        self.res += 1
                cur = len(queue)

        res = []
        self.res = 1
        for i in range(n):
            bfs(i)
            res.append(self.res)
            self.res = 1
        return res

思路2

参考自：https://leetcode-cn.com/circle/discuss/TgHsJg/ 中 Heltion 的讨论。

对每个点统计子树节点某个值的和的问题,只需要在DFS过程中累加值,每个点离开的时候的值减去每个点进来的时候的值就是答案。复杂度是O(n)。

无向图的邻接表应两个方向都要做。

代码2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution:
    def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:
        adj = collections.defaultdict(list)
        for e in edges:
            adj[e[0]].append(e[1])
            adj[e[1]].append(e[0])
         
        def dfs(node, parent = -1):
            res[node] -= cnt[labels[node]]
            cnt[labels[node]] += 1
            for next in adj[node]:
                if next != parent:
                    dfs(next, node)
            res[node] += cnt[labels[node]]

        res = [0] * n
        cnt = collections.defaultdict(int)
        dfs(0)
        return res

最多的不重叠子字符串

给你一个只包含小写字母的字符串 s ，你需要找到 s 中最多数目的非空子字符串，满足如下条件：

这些字符串之间互不重叠，也就是说对于任意两个子字符串 s[i..j] 和 s[k..l] ，要么 j < k 要么 i > l 。 如果一个子字符串包含字符 ch ，那么 s 中所有 ch 字符都应该在这个子字符串中。 请你找到满足上述条件的最多子字符串数目。如果有多个解法有相同的子字符串数目，请返回这些子字符串总长度最小的一个解。可以证明最小总长度解是唯一的。

请注意，你可以以 任意 顺序返回最优解的子字符串。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-number-of-non-overlapping-substrings

示例

输入：s = “adefaddaccc”
输出：[“e”,“f”,“ccc”]
解释：下面为所有满足第二个条件的子字符串：
[
  “adefaddaccc”
  “adefadda”,
  “ef”,
  “e”,
“f”,
  “ccc”,
]
如果我们选择第一个字符串，那么我们无法再选择其他任何字符串，所以答案为 1 。如果我们选择 “adefadda” ，剩下子字符串中我们只可以选择 “ccc” ，它是唯一不重叠的子字符串，所以答案为 2 。同时我们可以发现，选择 “ef” 不是最优的，因为它可以被拆分成 2 个子字符串。所以最优解是选择 [“e”,“f”,“ccc”] ，答案为 3 。不存在别的相同数目子字符串解。

思路1

参考自：https://leetcode.com/problems/maximum-number-of-non-overlapping-substrings/discuss/743223/C%2B%2BJava-Greedy-O(n)

贪心：如果找到一个有效子串，然后又找到另一个和该有效子串重叠的有效子串，则丢弃掉较长的那个有效子串；例如，先找到"abccba”，接着找到"bccb”，接着找到"cc”，最后只保留"cc”。

1、首先，用数组l和r记录26个字母在字符串中的左边第一个索引和右边第一个索引；
2、然后，遍历字符串，当前字符s[i]的左索引为i，则有：

  • 用自定义的check()函数找以s[i]起始的子串右边界，如果check过程中发现有字符应该出现在i的左边，这说明没有以s[i]起始的合法子串。
  • 如果check到一个合法子串，则加入res，并记录其右边界索引。
  • 重复该逻辑，直到找到一个最小右边界的有效子串

3、如果左索引i在上一个有效子串的右边界索引之后，说明上一个有效子串将不会与后边的有效子串发生重叠，则上一个有效子串将永久地记录入答案。

代码1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

class Solution:
    def maxNumOfSubstrings(self, s: str):
        def check(s, i, l, r):
            right = r[ord(s[i]) - ord("a")]

            # # 循环上界会在循环过程中更新，此时Python应用while循环
            # # for循环会出错，因为上界不会更新，只会在初始上界处停止
            # for j in range(i, right+1):
            #     if l[ord(s[j]) - ord("a")] < i:
            #         return -1
            #     right = max(right, r[ord(s[j]) - ord("a")])

            j = i
            while j <= right:
                if l[ord(s[j]) - ord("a")] < i:
                    return -1
                right = max(right, r[ord(s[j]) - ord("a")])
                j += 1

            return right

        l = [float("inf")] * 26
        r = [float("-inf")] * 26
        res = [1]
        for i in range(len(s)):
            l[ord(s[i]) - ord("a")] = min(l[ord(s[i]) - ord("a")], i)
            r[ord(s[i]) - ord("a")] = max(r[ord(s[i]) - ord("a")], i)
        right = float("inf")
        for i in range(len(s)):
            if i == l[ord(s[i]) - ord("a")]:
                new_right = check(s, i, l, r)
                if new_right != -1:
                    if i > right:
                        res.append("")
                    right = new_right
                    res[-1] = s[i:right+1]
        return res

找到最接近目标值的函数值

Winston 构造了一个如上所示的函数 func 。他有一个整数数组 arr 和一个整数 target ，他想找到让 |func(arr, l, r) - target| 最小的 l 和 r 。

请你返回 |func(arr, l, r) - target| 的最小值。

请注意， func 的输入参数 l 和 r 需要满足 0 <= l, r < arr.length 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-a-value-of-a-mysterious-function-closest-to-target

示例

输入：arr = [9,12,3,7,15], target = 5
输出：2
解释：所有可能的 [l,r] 数对包括 [ [0,0],[1,1],[2,2],[3,3],[4,4],[0,1],[1,2],[2,3],[3,4],[0,2],[1,3],[2,4],[0,3],[1,4],[0,4] ]， Winston 得到的相应结果为 [9,12,3,7,15,8,0,3,7,0,0,3,0,0,0] 。最接近 5 的值是 7 和 3，所以最小差值为 2 。

思路1

参考自：https://leetcode.com/problems/find-a-value-of-a-mysterious-function-closest-to-target/discuss/743381/Python-6-lines-O(nlogm)-solution

代码1

1
2
3
4
5
6
7
8

class Solution:
    def closestToTarget(self, arr: List[int], target: int) -> int:
        s, ans = set(), float('inf')
        for a in arr:
            s = {a & b for b in s} | {a}
            for c in s:
                ans = min(ans, abs(c - target))
        return ans

总结

仅AC第1题。
目前全国排名 2221 ，全球排名 10343 。
得分 3 / 21 ，未完成，全国排名 2782 / 5779 。这次状态不好，题也比较trick，所以比较惨，排名估计会掉挺多。
1、0:14:07，模拟题签到都花了14分钟，这次状态太差了。
2、未完成，无向图做邻接表再DFS，其中DFS比较trick。首先没有考虑无向图的双向性，以及忽视了0必为根节点这一条件，WA了无数次；同时因为上周的教训，这次用了BFS，BFS思路在之后修正了前面的两个问题后依然超时。
3、未完成，贪心思想，在比赛中思路大致方向是对的，即先find()和rfind()包含特定字符的子串左右边界，再贪心地留下其中最短的不重叠的合法子串。但是一些细节逻辑上没能处理好，确实还是比较绕的一题。
4、未完成。因为明早要面试，这题未复盘。