目录

统计好三元组

给你一个整数数组 arr ，以及 a、b 、c 三个整数。请你统计其中好三元组的数量。

如果三元组 (arr[i], arr[j], arr[k]) 满足下列全部条件，则认为它是一个 好三元组 。

  • 0 <= i < j < k < arr.length
  • |arr[i] - arr[j]| <= a
  • |arr[j] - arr[k]| <= b
  • |arr[i] - arr[k]| <= c

其中 |x| 表示 x 的绝对值。

返回 好三元组的数量 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/count-good-triplets

示例

输入：arr = [3,0,1,1,9,7], a = 7, b = 2, c = 3
输出：4
解释：一共有 4 个好三元组：[(3,0,1), (3,0,1), (3,1,1), (0,1,1)] 。

思路1

签到题，按题意暴力枚举。

代码1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class Solution:
    def countGoodTriplets(self, arr: List[int], a: int, b: int, c: int) -> int:
        n = len(arr)
        res = 0
        for i in range(n):
            for j in range(i+1, n):
                for k in range(j+1, n):
                    if abs(arr[i] - arr[j]) <= a and abs(arr[j] - arr[k]) <= b and abs(arr[i] - arr[k])<= c:
                        res += 1
        return res

找出数组游戏的赢家

给你一个由 不同 整数组成的整数数组 arr 和一个整数 k 。

每回合游戏都在数组的前两个元素（即 arr[0] 和 arr[1] ）之间进行。比较 arr[0] 与 arr[1] 的大小，较大的整数将会取得这一回合的胜利并保留在位置 0 ，较小的整数移至数组的末尾。当一个整数赢得 k 个连续回合时，游戏结束，该整数就是比赛的 赢家 。

返回赢得比赛的整数。

题目数据 保证 游戏存在赢家。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-the-winner-of-an-array-game

示例

输入：arr = [2,1,3,5,4,6,7], k = 2
输出：5
解释：一起看一下本场游戏每回合的情况： 因此将进行 4 回合比赛，其中 5 是赢家，因为它连胜 2 回合。

思路1

按题意模拟，出于减少时间复杂度的目的，将给定数组转成双端队列(deque)。

每次从队列头部pop出前两个数进行比较。如果第一个数较大，则把第一个数append回队列头部，把第二个数append到队列末尾；否则把第一个数append到队列末尾，把第二个数append到队列头部。同时，如果第一个数较大，说明该数处于连胜中，统计连胜数，到达k值时说明该数胜出；如果第二个数较大，说明新的数取代了上一次的赢家，将连胜数回落到1。

同时，用一个O(n)找数组的最大值，如果第一个数是最大值则直接返回该最大值。双端队列pop()和append()都是O(1)，故整体时间复杂度为O(n)。

代码1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution:
    def getWinner(self, arr: List[int], k: int) -> int:
        maxx = max(arr)
        tmp = collections.deque(arr)
        fst = tmp.popleft()
        snd = tmp.popleft()
        if fst > snd:
            tmp.appendleft(fst)
            tmp.append(snd)
            pre = fst
        else:
            tmp.appendleft(snd)
            tmp.append(fst)
        cnt = 1
        while True:
            if tmp[0] == maxx:
                return maxx
            if cnt == k:
                return tmp[0]
            fst = tmp.popleft()
            snd = tmp.popleft()
            if fst > snd:
                tmp.appendleft(fst)
                tmp.append(snd)
                cnt += 1
            else:
                tmp.appendleft(snd)
                tmp.append(fst)
                cnt = 1

思路2

每次比较完后，直接将较大值放在第二个数的位置，向后遍历整个数组。一次遍历O(n)。

代码2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

class Solution:
    def getWinner(self, arr: List[int], k: int) -> int:
        idx, cnt = 0, 0
        while cnt < k and idx < len(arr) - 1:
            if arr[idx] > arr[idx+1]:
                arr[idx+1] = arr[idx]
                cnt += 1
            else:
                cnt = 1
            idx += 1
        return arr[idx]

排布二进制网格的最少交换次数

给你一个 n x n 的二进制网格 grid，每一次操作中，你可以选择网格的 相邻两行 进行交换。

一个符合要求的网格需要满足主对角线以上的格子全部都是 0 。

请你返回使网格满足要求的最少操作次数，如果无法使网格符合要求，请你返回 -1 。

主对角线指的是从 (1, 1) 到 (n, n) 的这些格子。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-swaps-to-arrange-a-binary-grid

示例

示例1：

输入：grid = [[0,0,1],[1,1,0],[1,0,0]]
输出：3

思路1

这题花了50分钟，还WA了3次，最初的思路错了。

作为教训，先记录最初的错误思路：记录每行末尾0的个数，然后越在前面的行，需要的0越多。具体地，要构成一个下三角矩阵，第i行（i从0开始）需要的0的个数为n-i-1个。因此对每行0的个数做一个降序排序，且采用冒泡排序的思想。冒泡排序做成一个排序数列，最少的交换次数等于原数列中的逆序对数，因为n很小，直接暴力计算逆序对数即可。

错误原因：有些情况并不需要把每行0的个数构成一个降序数列，因为在这些情况中，0的个数是富余的，例如以下示例：

[[1,0,0,0,0,0],
[0,1,0,1,0,0],
[1,0,0,0,0,0],
[1,1,1,0,0,0],
[1,1,0,1,0,0],
[1,0,0,0,0,0]]

每行0的个数统计为[5,2,5,3,2,5]，有5个逆序对。而实际上，只需将第2行先与第3行交换，然后再与第4行交换即可构成下三角矩阵，只需交换2次，而非5次。

正确思路：依然统计每行末尾0的个数，因为知道构造下三角矩阵每行需要的0的个数，因此找到需要第i行0的个数最近的那一行位置pos，然后把第i行交换到第pos行即可（贪心思想）；如果第i行0的个数无法满足任何一行对0的个数的要求，这说明无法构成下三角矩阵。其中实际模拟了交换的过程，这其实对我来说是挺难想到的。

正确思路参考自：https://www.2cto.com/kf/201310/251875.html

代码1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

class Solution:
    def minSwaps(self, grid) -> int:
        n = len(grid)
        tmp = [] # 统计每行末尾0的个数
        for i in range(n):
            cnt = 0
            hasOne = False
            for j in range(n-1, -1, -1):
                if grid[i][j] == 0:
                    cnt += 1
                else:
                    hasOne = True
                    tmp.append(cnt)
                    break
            if not hasOne:
                tmp.append(n)
        res = 0
        for i in range(n):
            pos = -1
            for j in range(i, n):
                if tmp[j] >= n - i - 1:
                    pos = j # 找拥有tmp[i]个0的第i行应该交换到的最近的行
                    break
            if pos == -1:
                return -1 # 找不到则说明无法构造下三角矩阵
            for j in range(pos, i, -1):
                # 模拟相邻行交换过程，直到第i行交换到之前找到的pos的位置
                tmp[j], tmp[j-1] = tmp[j-1], tmp[j] 
                res += 1
        return res

最大得分

你有两个 有序 且数组内元素互不相同的数组 nums1 和 nums2 。

一条 合法路径 定义如下：

选择数组 nums1 或者 nums2 开始遍历（从下标 0 处开始）。 从左到右遍历当前数组。 如果你遇到了 nums1 和 nums2 中都存在的值，那么你可以切换路径到另一个数组对应数字处继续遍历（但在合法路径中重复数字只会被统计一次）。 得分定义为合法路径中不同数字的和。

请你返回所有可能合法路径中的最大得分。

由于答案可能很大，请你将它对 10^9 + 7 取余后返回。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/get-the-maximum-score

示例

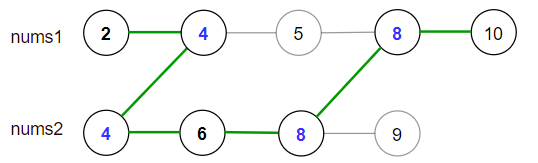
输入：nums1 = [2,4,5,8,10], nums2 = [4,6,8,9]
输出：30
解释：合法路径包括：
[2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10],（从 nums1 开始遍历） [4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10] （从 nums2 开始遍历） 最大得分为上图中的绿色路径 [2,4,6,8,10] 。

思路1

归并排序思想的一种动态规划：dp[0][i]和dp[1][i]分表表示在路过第1个数组和第2个数组第i个数时的最大得分。两个数组各有一个指针指到其可访问节点。

  • 如果两个指针所指数不等，则较小数那个指针需要往前移动一步，同时该数组上的dp要转移状态，假设这时是第一个数组较小，则有dp[0][i] = dp[0][i-1] + nums[i]
  • 难点：两个指针所指数相等，两个数组可以切换到对方，则选取得分较大的一条路径。因为两条路都能到达这个位置，所以两条路的得分都统一为较大的那个值（比赛时没想到这点，比赛时分别讨论两条路的情况，没做出来）。这里包含贪心思想。

最后跟归并一样，两个数组其中一个遍历完后，还需要将剩下那个没遍历完的也遍历掉。遍历了两个数组，时间复杂度O(n+m)。

代码1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution:
    def maxSum(self, nums1, nums2) -> int:
        # dp[0][i]: 遍历到第1个数组的第i个数时的最大和值
        # dp[1][i]: 遍历到第2个数组的第i个数时的最大和值
        n, m = len(nums1), len(nums2)
        dp = [[0] * max(n + 1, m + 1) for _ in range(2)]
        left, right = 1, 1
        while left < n + 1 and right < m + 1:
            if nums1[left - 1] > nums2[right - 1]:
                dp[1][right] = dp[1][right - 1] + nums2[right - 1]
                right += 1
            elif nums1[left - 1] < nums2[right - 1]:
                dp[0][left] = dp[0][left - 1] + nums1[left - 1]
                left += 1
            else:
                best = max(dp[0][left - 1], dp[1][right - 1]) + nums1[left - 1]
                dp[0][left] = dp[1][right] = best
                left += 1
                right += 1

        while left < n + 1:
            dp[0][left] = dp[0][left - 1] + nums1[left - 1]
            left += 1
        while right < m + 1:
            dp[1][right] = dp[1][right - 1] + nums2[right - 1]
            right += 1
        return max(max(dp[0]), max(dp[1])) % int(1e9+7)

思路2

思路与思路1相同，不过优化了动态规划的维度。

代码2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution:
    def maxSum(self, nums1, nums2) -> int:
        n, m = len(nums1), len(nums2)
        i, j = 0, 0
        t1, t2 = 0, 0
        while i < n and j < m:
            if nums1[i] < nums2[j]:
                t1 += nums1[i]
                i += 1
            elif nums1[i] > nums2[j]:
                t2 += nums2[j]
                j += 1
            else:
                best = max(t1, t2) + nums1[i]
                t1 = t2 = best
                i += 1
                j += 1
        while i < n:
            t1 += nums1[i]
            i += 1
        while j < m:
            t2 += nums2[j]
            j += 1
        return max(t1, t2) % int(1e9+7)

总结

AC前3题。
目前全国排名 2799 ，全球排名 12252 。
得分 12 / 18 ，未完成，全国排名 1053 / 5474，全球排名 2652 / 15382。
1、0:02:57，签到题，暴力枚举；
2、0:11:52，WA了1次，k=1的情况粗心没照顾好。模拟题。
3、1:01:06，WA了3次，思路一开始是错误的，之后通过百度才拿到正确思路AC。
4、未完成，比赛时整体思路方向正确，两数组切换的情况没处理好，主要还是代码写复杂了，要照顾的细节一多脑子就乱了。

因为目前基本算是没有刷题需求了，而这次刚好是第200场周赛，算是一个完整的谢幕吧。以后如果实在闲得没事干，就继续刷和复盘。