目录

两个相同字符之间的最长子字符串

给你一个字符串 s，请你返回 两个相同字符之间的最长子字符串的长度 ，计算长度时不含这两个字符。如果不存在这样的子字符串，返回 -1 。

子字符串 是字符串中的一个连续字符序列。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/largest-substring-between-two-equal-characters

示例

输入：s = “cabbac”
输出：4
解释：最优的子字符串是 “abba” ，其他的非最优解包括 “bb” 和 "” 。

思路1

对每个字符，向后遍历字符串，遇到与当前字符一样的，则计算相同字符间的子字符串长度，保留最大值。

代码1

1
2
3
4
5
6
7
8

class Solution:
    def maxLengthBetweenEqualCharacters(self, s: str) -> int:
        res = -1
        for i in range(len(s)-1):
            for j in range(i+1, len(s)):
                if s[i] == s[j]:
                    res = max(res, j - i - 1)
        return res

执行操作后字典序最小的字符串

给你一个字符串 s 以及两个整数 a 和 b 。其中，字符串 s 的长度为偶数，且仅由数字 0 到 9 组成。

你可以在 s 上按任意顺序多次执行下面两个操作之一：

  • 累加：将  a 加到 s 中所有下标为奇数的元素上（下标从 0 开始）。数字一旦超过 9 就会变成 0，如此循环往复。例如，s = “3456” 且 a = 5，则执行此操作后 s 变成 “3951”。
  • 轮转：将 s 向右轮转 b 位。例如，s = “3456” 且 b = 1，则执行此操作后 s 变成 “6345”。 请你返回在 s 上执行上述操作任意次后可以得到的 字典序最小 的字符串。

如果两个字符串长度相同，那么字符串 a 字典序比字符串 b 小可以这样定义：在 a 和 b 出现不同的第一个位置上，字符串 a 中的字符出现在字母表中的时间早于 b 中的对应字符。例如，“0158” 字典序比 “0190” 小，因为不同的第一个位置是在第三个字符，显然 ‘5’ 出现在 ‘9’ 之前。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/lexicographically-smallest-string-after-applying-operations

示例

输入：s = “74”, a = 5, b = 1
输出：“24”
解释：执行操作如下：
初态：“74”
轮转：“47”
累加：“42”
轮转：“24"​​​​​​​​​​​​
无法获得字典序小于 “24” 的字符串。

思路1

暴力DFS尝试每种可能性。

代码1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution:
    def findLexSmallestString(self, s: str, a: int, b: int) -> str:
        n = len(s)
        self.tmp = set()
        self.res = s
        
        def dfs(s):
            if s in self.tmp:
                return
            self.tmp.add(s)
            v = s[b:] + s[:b]
            self.res = min(self.res, v)
            dfs(v)
            s = list(s)
            for i in range(1, n, 2):
                s[i] = chr(ord("0") + (ord(s[i]) - ord("0") + a) % 10)
            s = "".join(s)
            self.res = min(self.res, s)
            dfs(s)
        
        dfs(s)
        return self.res

无矛盾的最佳球队

假设你是球队的经理。对于即将到来的锦标赛，你想组合一支总体得分最高的球队。球队的得分是球队中所有球员的分数 总和 。

然而，球队中的矛盾会限制球员的发挥，所以必须选出一支 没有矛盾 的球队。如果一名年龄较小球员的分数 严格大于 一名年龄较大的球员，则存在矛盾。同龄球员之间不会发生矛盾。

给你两个列表 scores 和 ages，其中每组 scores[i] 和 ages[i] 表示第 i 名球员的分数和年龄。请你返回 所有可能的无矛盾球队中得分最高那支的分数 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/best-team-with-no-conflicts

示例

输入：scores = [1,2,3,5], ages = [8,9,10,1]
输出：6 解释：最佳的选择是前 3 名球员。

思路1

贪心+动态规划：先按分数升序排序，再按年龄升序排序，dp[i]表示前i个球员且选择第i个球员的最大分数。对每个dp[i]，设初值为第i个球员的分数，向前遍历，遇到年龄小于等于第i个球员的第j个球员，有分数等于dp[j]+第i个球员的分数，取其中最大值作为dp[i]。

代码1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution:
    def bestTeamScore(self, scores: List[int], ages: List[int]) -> int:
        tmp = sorted(zip(scores, ages))
        n = len(tmp)
        dp = [0] * n
        dp[0] = tmp[0][0]
        for i in range(1, n):
            dp[i] = tmp[i][0]
            for j in range(i):
                if tmp[j][1] <= tmp[i][1]:
                    dp[i] = max(dp[i], tmp[i][0] + dp[j])
        return max(dp)

带阈值的图连通性

有 n 座城市，编号从 1 到 n 。编号为 x 和 y 的两座城市直接连通的前提是： x 和 y 的公因数中，至少有一个 严格大于 某个阈值 threshold 。更正式地说，如果存在整数 z ，且满足以下所有条件，则编号 x 和 y 的城市之间有一条道路：

  • x % z == 0
  • y % z == 0
  • z > threshold

给你两个整数 n 和 threshold ，以及一个待查询数组，请你判断每个查询 queries[i] = [ai, bi] 指向的城市 ai 和 bi 是否连通（即，它们之间是否存在一条路径）。

返回数组 answer ，其中answer.length == queries.length 。如果第 i 个查询中指向的城市 ai 和 bi 连通，则 answer[i] 为 true ；如果不连通，则 answer[i] 为 false 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/graph-connectivity-with-threshold

示例

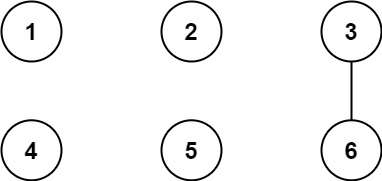
输入：n = 6, threshold = 2, queries = [[1,4],[2,5],[3,6]]
输出：[false,false,true]
解释：每个数的因数如下：
1: 1
2: 1, 2
3: 1, 3
4: 1, 2, 4
5: 1, 5
6: 1, 2, 3, 6
所有大于阈值的的因数已经加粗标识，只有城市 3 和 6 共享公约数 3 ，因此结果是：
[1,4] 1 与 4 不连通
[2,5] 2 与 5 不连通
[3,6] 3 与 6 连通，存在路径 3–6

思路1

并查集

代码1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import math

class Solution:
    def areConnected(self, n: int, t: int, q: List[List[int]]) -> List[bool]:
        ufs = {i: i for i in range(n + 1)}

        def find(x):
            nonlocal ufs
            if x == ufs[x]:
                return x
            t = find(ufs[x])
            ufs[x] = t
            return ufs[x]

        for i in range(t + 1, n + 1):
            for j in range(1, int(math.sqrt(i)) + 1):
                if i % j == 0:
                    if j > t:
                        ufs[find(i)] = find(j)
                    if i // j > t:
                        ufs[find(i)] = find(i // j)
        ans = []
        for i, j in q:
            ans.append(find(i) == find(j))
        return ans

总结

久不刷题，只能签到第1题了。